Question

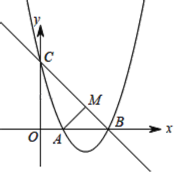
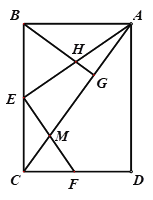
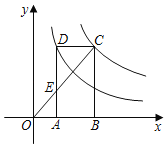
【题目】如图，矩形ABCD的顶点C，D分别在反比例函数y＝（x＞0）．y＝（x＞0）的图象上，顶点A，B在x轴上，连接OC，交DA于点E，则＝_____．

Answer 1

【答案】

【解析】

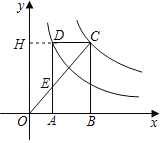
根据反比例函数图象上点的坐标特征以及反比例函数k的几何意义，求出矩形CBOH的面积为8，矩形ADHO的面积为3，进一步求得OA：CD=3：5，通过证得△AOE∽△DCE，得出＝＝．

解：延长CD交y轴于点H，

∵点C在反比例函数y＝（x＞0）的图象上，

∴矩形CBOH的面积为8，

∵点D在反比例函数y＝（x＞0）的图象上，

∴矩形ADHO的面积为3，

∴矩形ABCD的面积为：8﹣3＝5，

∴OA：CD＝3：5，

∵CD∥OA，

∴△AOE∽△DCE，

∴＝＝，

故答案为：．