题目内容
【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为
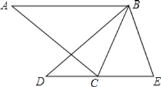
A. 36° B. 40° C. 45° D. 50°
【答案】A
【解析】先根据旋转的性质可知BE=BC,∠BED=∠ACB=72°,∠ABC=∠EBD,再根据等腰三角形的性质和三角形内角和的性质可求得∠EBC= 36°,从而得出∠ABD=36°.
∵△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),
∴BE=BC,∠BED=∠ACB=72°∠ABC=∠EBD.
∴∠ABC-∠DBC =∠EBD-∠DBC.
即:∠ABD=∠EBC。
∵BE=BC,
∴∠BCE=∠BEC=72°.
在△BCE中,∠BCE+∠BEC+∠CBE=180°,
∴∠CBE=36°,
∴∠ABD=∠EBC=36°.
故选A.

练习册系列答案
相关题目