题目内容
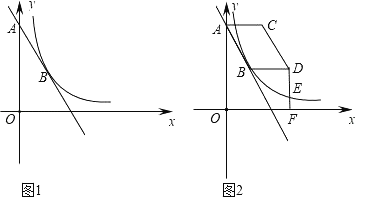
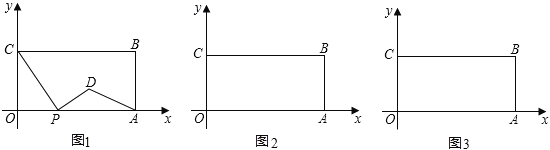
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA、OC分别在x轴、y轴的正半轴上,OA=4,OC=2.点P从点O出发,沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段CP的中点绕点P按顺时针方向旋转90°得点D,点D随点P的运动而运动,连接DP、DA.
(1)当t=2时,点D的坐标是 ;
(2)请用含t的代数式表示出点D的坐标 ;
(3)在点P从O向A运动的过程中,△DPA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
【答案】(1)D(![]() ,
,![]() )(2)D(
)(2)D(![]() ,
,![]() )(3)t=2或3秒.
)(3)t=2或3秒.
【解析】
(1)由已知可得点![]()
![]() , 再求出
, 再求出![]() 的中点坐标,根据相似的性质即可求出
的中点坐标,根据相似的性质即可求出![]() 点坐标;(2)设出
点坐标;(2)设出![]() 点坐标, 再求出
点坐标, 再求出![]() 的中点坐标, 根据相似的性质即可求出
的中点坐标, 根据相似的性质即可求出![]() 点坐标;
点坐标;
(3)分类讨论,先判断出可能为直角的角, 再根据勾股定理求解;
解: (1)![]() 点
点![]() 从点
从点![]() 出发, 沿
出发, 沿![]() 轴以每秒 1 个单位长的速度向点
轴以每秒 1 个单位长的速度向点![]() 匀速运动,过
匀速运动,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,
,
![]() ,而
,而![]() ,
,
∴![]() ,
,![]() ,
,
∵线段CP的中点绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得点
得点![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴OE=OP+PE=3
![]() 点坐标为
点坐标为![]() ;
;
(2)![]() 点
点![]() 从点
从点![]() 出发, 沿
出发, 沿![]() 轴以每秒 1 个单位长的速度向点
轴以每秒 1 个单位长的速度向点![]() 匀速运动,
匀速运动,
![]() ,而
,而![]() ,
,
![]() ,
,
∵![]() 的中点绕点
的中点绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得点
得点![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴![]()
![]() 点坐标为
点坐标为![]() ;
;
(3) 能构成直角三角形 .
①当![]() 时,
时,![]() ,
,
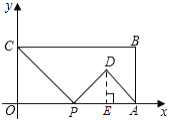
由勾股定理得,![]() ,
,![]() ,
,![]() ,
,
即![]() ,
,
解得,![]() 或
或![]() (舍 去) .
(舍 去) .
![]() 秒 .
秒 .
②当![]() 时, 此时点
时, 此时点![]() 在
在![]() 上,
上,
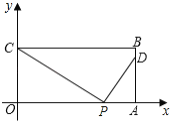
可知,![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,![]() 秒 .
秒 .
综上, 可知当![]() 为 2 秒或 3 秒时,
为 2 秒或 3 秒时,![]() 能成为直角三角形 .
能成为直角三角形 .

 名校课堂系列答案
名校课堂系列答案【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚