题目内容
【题目】在一元二次方程中,有著名的韦达定理:对于一元二次方程ax2+bx+c=0(a≠0),如果方程有两个实数根x1,x2,那么x1+x2=![]() ,x1+x2=
,x1+x2=![]() (说明:定理成立的条件△≥0).比如方程2x2-3x-1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=
(说明:定理成立的条件△≥0).比如方程2x2-3x-1=0中,△=17,所以该方程有两个不等的实数解.记方程的两根为x1,x2,那么x1+x2=![]() ,x1+x2=
,x1+x2=![]() .请阅读材料回答问题:
.请阅读材料回答问题:
(1)已知方程x2-3x-2=0的两根为x1、x2,求下列各式的值:
①x12+x22;②![]() ;
;
(2)已知x1,x2是一元二次方程4kx2-4kx+k+1=0的两个实数根.
①是否存在实数k,使(2x1-x2)(x1-2x2)=![]() 成立?若存在,求出k的值;若不存在,请说明理由;
成立?若存在,求出k的值;若不存在,请说明理由;
②求使![]() -2的值为整数的实数k的整数值.
-2的值为整数的实数k的整数值.
【答案】(1)①13;②-![]() ;(2)见解析;②k=-2或-3或-5.
;(2)见解析;②k=-2或-3或-5.
【解析】
(1)用韦达定理写出x1+x2与x1x2的值,把(x1+x2)2进行完全平方公式变形求得①,通分求值求得②.
(2)先求出△>0时,k的取值范围,用韦达定理写出用k表示x1+x2与x1x2的值.①直接把等式左边展开变形,代入x1+x2与x1x2的式子,即求出k.②化简式子得到k在分母的分式,根据式子的值为整数和k的取值范围确定k的值.
解:(1)∵x2-3x-2=0,△=(-3)2-4×(-2)=17>0,∴x1+x2=3,x1x2=-2
①x12+x22=(x1+x2)2-2x1x2=32-2×(-2)=9+4=13;
②![]() =
=![]() =-
=-![]() ;
;
(2)∵方程有两个实数根,
∴△=(-4k)2-44k(k+1)>0;
∴k<0,x1+x2=1,x1x2=![]() ,
,
①∵(2x1-x2)(x1-2x2)=2x12-5x1x2+2x22=2(x12+2x1x2+x22)-9x1x2=2(x1+x2)2-9x1x2,
∴2-9![]() =
=![]() ,
,
解得:k=![]() ,与k<0矛盾;
,与k<0矛盾;
∴不存在k的值,使(2x1-x2)(x1-2x2)=-![]() 成立.
成立.
②![]() -2=
-2=![]() =
=![]() =
=![]() =
=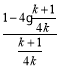 =
=![]() =
=![]() .
.
∵![]() -2=
-2=![]() 的值为整数,
的值为整数,
∴k+1=±1或±2或±4,
又∵k<0,
∴k=-2或-3或-5.