Question

【题目】已知，在Rt中，，点是斜边的中点，，且，于点，联结．

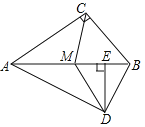
（1）求证： ；

（2）当时，求的值；

（3）在（2）的条件下，求的值．

Answer 1

【答案】（1）见解析；（2）S△BED：S△MED=1：3；（3）cos∠ABC=．

【解析】

（1）易证∠DME=∠CBA，∠ACB=∠MED=90°，从而可证明△MED∽△BCA；

（2）由∠ACB=90°，点M是斜边AB的中点，可知MB=MC=AM，从而可证明MD=CM=MB=AB，从而证得S△AMC=S△BNC=S△ABC，由S△BDM=证得，从而证得S△BED：S△MED=1：3；

（3）由，得到，进一步得到，证得cos∠EMD=，由∠DME=∠CBA，证得cos∠ABC=．

解：（1）∵MD∥BC，

∴∠DME=∠CBA，

∵∠ACB=∠MED=90°，

∴△MED∽△BCA，

（2）∵∠ACB=90°，点M是斜边AB的中点，

∴MB=MC=AM=AB，

∵MC=MD，

∴MD=AB，

∴S△AMC=S△BNC=S△ABC，

∵△MED∽△BCA，

∴=（）2=，

∵S△BDM=，

∴，

∴S△BED：S△MED=1：3；

（3）∵，

∴，

∵MD=MB，

∴，

∴cos∠EMD=，

∵∠DME=∠CBA，

∴cos∠ABC=．