Question

【题目】探究活动一：

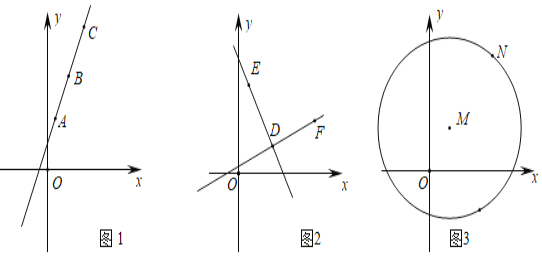
如图1，某数学兴趣小组在研究直线上点的坐标规律时，在直线AB上的三点A（1，3）、B（2，5）、C（4，9），有kAB＝＝2，kAC＝＝2，发现kAB＝kAC，兴趣小组提出猜想：若直线y＝kx+b（k≠0）上任意两点坐标P（x1，y1），Q（x2，y2）（x1≠x2），则kPQ＝是定值．通过多次验证和查阅资料得知，猜想成立，kPQ是定值，并且是直线y＝kx+b（k≠0）中的k，叫做这条直线的斜率．

请你应用以上规律直接写出过S（﹣2，﹣2）、T（4，2）两点的直线ST的斜率kST＝ ．

探究活动二

数学兴趣小组继续深入研究直线的“斜率”问题，得到正确结论：任意两条不和坐标轴平行的直线互相要直时，这两条直线的斜率之积是定值．

如图2，直线DE与直线DF垂直于点D，D（2，2），E（1，4），F（4，3）．请求出直线DE与直线DF的斜率之积．

综合应用

如图3，⊙M为以点M为圆心，MN的长为半径的圆，M（1，2），N（4，5），请结合探究活动二的结论，求出过点N的⊙M的切线的解析式．

Answer 1

【答案】探究活动一：；探究活动二：﹣1；综合应用：y＝﹣x+9．

【解析】

（1）直接利用公式计算即可；

（2）运用公式分别求出kDE和kDF的值，再计算kDE×kDF＝﹣1；

（3）先求直线MN的斜率kMN，根据切线性质可知PQ⊥MN，可得直线PQ的斜率kPQ，待定系数法即可求得直线PQ解析式．

解：（1）∵S（﹣2，﹣2）、T（4，2）

∴kST＝＝

故答案为：

（2）∵D（2，2），E（1，4），F（4，3）．

∴kDE＝＝﹣2，kDF＝＝，

∴kDE×kDF＝﹣2×＝﹣1，

∴任意两条不和坐标轴平行的直线互相垂直时，这两条直线的斜率之积等于﹣1．

（3）设经过点N与⊙M的直线为PQ，解析式为y＝kPQx+b

∵M（1，2），N（4，5），

∴kMN＝＝1，

∵PQ为⊙M的切线

∴PQ⊥MN

∴kPQ×kMN＝﹣1，

∴kPQ＝﹣1，

∵直线PQ经过点N（4，5），

∴5＝﹣1×4+b，解得 b＝9

∴直线PQ的解析式为y＝﹣x+9．