题目内容
【题目】如图,矩形ABCD,点E, F分别在AD、BC上且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,若AB=![]() ,则CG为( )
,则CG为( )
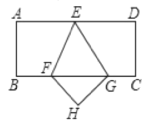
A.3.B.1.C.2.D.![]() .
.
【答案】B
【解析】
连接AF,根据矩形的性质、平行线的性质结合折叠的性质可得出∠AEF=∠AFE,即AF=AE,设BF=2x,则AD=BC=6x,AF=AE=FG=3x,CG=BC-BF-FG=x,在Rt△ABF中,利用勾股定理可求出x的值,此题得解.
连接AF,如图所示,
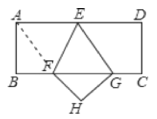
∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
∴∠AEF=∠GFE.
由折叠的性质可知:AB=HG,BF=HF,∠ABF=∠GHF=90°,∠BFE=∠HFE,
∴△ABF≌△GHF,
∴AF=FG,∠AFB=∠GFH,
∴∠AFE=∠GFE,
∴∠AEF=∠AFE,
∴AF=AE.
设BF=2x,则AD=BC=6x,AF=AE=FG=3x,CG=BCBFFG=x.
在Rt△ABF中,∠B=90°,AB=![]() ,AF=3x,BF=2x,
,AF=3x,BF=2x,
∴AF2=AB2+BF2,即(3x)2=(2x)2+(![]() )2,
)2,
解得:x=1或x=1(舍去),
∴CG=x=1.
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.