题目内容
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形,动点
的等边三角形,动点![]() 、
、![]() 同时从
同时从![]() 、
、![]() 两点出发,分别沿
两点出发,分别沿![]() 、
、![]() 方向匀速移动,它们的速度都是
方向匀速移动,它们的速度都是![]() ,当点
,当点![]() 到达点
到达点![]() 时,
时,![]() 、
、![]() 两点停止运动,设点
两点停止运动,设点![]() 的运动时间
的运动时间![]() .
.
解答下列各问题:
(1)求![]() 的面积
的面积
(2)当![]() 为何值时,
为何值时,![]() 是直角三角形?
是直角三角形?
(3)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的关系式;是否存在某一时刻
的关系式;是否存在某一时刻![]() ,使四边形
,使四边形![]() 的面积是
的面积是![]() 面积的三分之二?如果存在,求出
面积的三分之二?如果存在,求出![]() 的值;不存在请说明理由
的值;不存在请说明理由
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() ,不存在,理由见解析.
,不存在,理由见解析.
【解析】
(1)根据等边三角形的面积公式计算即可;
(2)先用t的代数式表示出BP,BQ,再分∠BPQ=90°和∠BQP=90°两种情况,在直角△BQP中根据BP,BQ的表达式和∠B的度数进行求解即可;
(3)先用t的代数式表示出△BPQ的面积,然后用△ABC的面积减去△BPQ的面积即得y与t的函数关系式;假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的![]() ,可得关于t的一元二次方程,再根据方程根的判别式即得结果.
,可得关于t的一元二次方程,再根据方程根的判别式即得结果.
解:(1)![]() 的面积=
的面积=![]() ;
;
(2)设经过t秒△PBQ是直角三角形,则AP=tcm,BQ=tcm,
在△ABC中,AB=BC=6cm,∠B=60°,∴BP=(6-t)cm,
若△PBQ是直角三角形,则∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=![]() BP,即t=
BP,即t=![]() (6-t),解得:t=2,
(6-t),解得:t=2,
当∠BPQ=90°时,BP=![]() BQ,即6-t=
BQ,即6-t=![]() t,解得:t=4,
t,解得:t=4,
∴当t=2或t=4时,△PBQ是直角三角形.
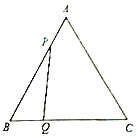
(3)过P作PM⊥BC于M,如图,
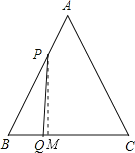
在△BPM中,∵sinB=![]() ,∴PM=PBsinB=
,∴PM=PBsinB=![]() (6-t),
(6-t),
∴S△PBQ=![]() BQPM=
BQPM=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴y与t的关系式为:y=![]() ;
;
假设存在某一时刻t,使得四边形APQC的面积是△ABC面积的![]() ,
,
则S四边形APQC=![]() S△ABC,∴
S△ABC,∴![]() =
=![]() ,
,
∴![]() ,∵(-6)2-4×1×12<0,∴方程无解,
,∵(-6)2-4×1×12<0,∴方程无解,
∴无论t取何值,四边形APQC的面积都不可能是△ABC面积的![]() .
.

【题目】今年上半年,住房和城乡建设等9部门决定在全国地级以上城市全面启动生活垃分类工作.圾分类有利于对垃圾进行分流处理,势在必行.为了了解同学们对垃圾分类相关知识的掌握情况,增强同学们的环保意识,西街中学团委对七年级一,二两班各69名学生进行了垃极分类相关知识的测试,并分别抽取了15份成绩,整理分析过程如下,请补充完整.
(收集数据)
一班15名学生测试成绩统计如下:(满分100分)
68,72,89,85,82,85,74,92,80,85,78,85,69,76,80
二班15名学生测试成绩统计如下:(满分100分)
86,89,83,76,73,78,67,80,80,79,80,84,82,80,83
(整理数据)
(1)按如下分数段整理、描述这两组样本数据
组别 频数 | 65.5~70.5 | 70.5~75.5 | 75.5~80.5 | 80.5~85.5 | 85.5~90.5 | 90.5~95.5 |
一 | 2 | 2 | 4 | 5 | 1 | 1 |
二 | 1 | 1 | a | b | 2 | 0 |
在表中,a= ,b= .
(分析数据)
(2)两组样本数据的平均数、众数、中位数、方差如下表所示:
班级 | 平均数 | 众数 | 中位数 | 方差 |
一 | 80 | x | 80 | 47.6 |
二 | 80 | 80 | y | z |
在表中:x= ,y= .
(3)若规定得分在80分及以上(含80分)为合格,请估计二班69名学生中垃极分类及投放相关知识合格的学生有 人.
(4)你认为哪个班的学生掌握垃圾分类相关知识的整体水平较好,说明理由.
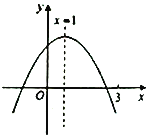
【题目】已知:二次函数![]()
![]() 中的
中的![]() 和
和![]() 满足下表:
满足下表:
| … |
| 0 | 1 | 2 | 3 | … |
| … | 3 | 0 |
| 0 | m | … |
(1) 观察上表可求得![]() 的值为________;
的值为________;
(2) 试求出这个二次函数的解析式;
(3) 若点A(n+2,y1),B(n,y2)在该抛物线上,且y1>y2,请直接写出n的取值范围.