题目内容
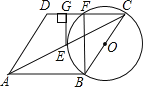
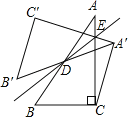
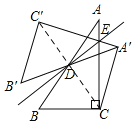
【题目】如图,点D是Rt△ABC斜边AB的中点,点E在边AC上.△A'B′C′与△ABC关于直线BE对称,连结A′C.且∠CA′C'=90°.若AC=4,BC=3.则AE的长为_____.
【答案】![]()
【解析】
由轴对称的性质和直角三角形斜边中线的性质得:CD=C'D=A'D=![]() AB=
AB=![]() A'B',证明△A'CC'≌△C'B'A'(HL),得A'C=C'B'=CB=3,设AE=x,则CE=4﹣x,根据勾股定理列方程可得结论.
A'B',证明△A'CC'≌△C'B'A'(HL),得A'C=C'B'=CB=3,设AE=x,则CE=4﹣x,根据勾股定理列方程可得结论.
解:连接CD,C'D,
∵∠CA'C'=90°,
由轴对称性质得:CD=C'D=A'D=![]() AB=
AB=![]() A'B',
A'B',
∴C、D、C'三点共线,
∴CC'=A'B',
∵△A'CC'≌△C'B'A'(HL),
∴A'C=C'B'=CB=3,
设AE=x,则CE=4﹣x,
∵AE=A'E,
在Rt△A'EC中,由勾股定理得:![]() ,
,
解得:![]()
∴AE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】某工厂要加工甲、乙、丙三种型号机械配件共120个,安排20个工人刚好一天加工完成,每人只加工一种配件,设加工甲种配件的人数为x,加工乙种配件的人数为y,根据下表提供的信息,解答下列问题:
配件种类 | 甲 | 乙 | 丙 |
每人每天加工配件的数量 | 8 | 6 | 5 |
每个配件获利 | 15 | 14 | 8 |
![]() 求y与x之间的关系.
求y与x之间的关系.
![]() 若这些机械配件共获利1420元,请求出加工甲、乙、丙三种型号配件的人数分别是多少人?
若这些机械配件共获利1420元,请求出加工甲、乙、丙三种型号配件的人数分别是多少人?