题目内容
【题目】如图,在A处的正东方向有一港口B.某巡艇从A处沿着北偏东60°方向巡逻,到达C处时接到命令,立刻在C处沿东南方向以20海里/小时的速度行驶3小时到达港口B.若取![]()
![]() 结果保留一位小数,则A,B间的距离为()
结果保留一位小数,则A,B间的距离为()
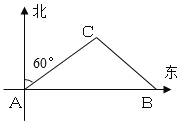
A.42.3海里B.73.5海里C.115.8海里D.119.9海里
【答案】C
【解析】
过点C作CD⊥AB于点D,根据题意可得,∠ACD=60°,∠BCD=45°,BC=20×3=60,然后根据锐角三角函数即可求出A,B间的距离.
解:如图,过点C作CD⊥AB于点D,
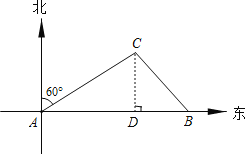
根据题意可知: ∠ACD=60°,∠BCD=45°,BC=20×3=60,
∴在Rt△BCD中,CD=BD=![]() BC=
BC=![]() ,
,
在Rt△ACD中,AD=CDtan60°=![]() ,
,
∴AB=AD+BD=![]() ≈115.8(海里).
≈115.8(海里).
答:A,B间的距离约为115.8海里.
故选:C.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:
类别 | 成本价(元/箱) | 销售价(元/箱) |
甲 | 25 | 35 |
乙 | 35 | 48 |
求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?