Question

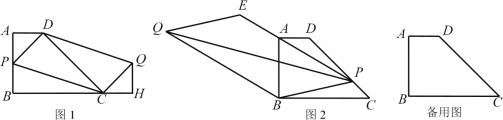
【题目】已知在四边形ABCD中，AD∥BC，AB⊥BC，AD＝2，AB＝4，BC＝6．

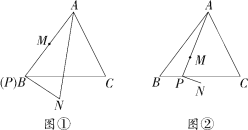
（1）如图1，P为AB边上一点，以PD，PC为边作平行四边形PCQD，过点Q作QH⊥BC，交BC的延长线于H．求证：△ADP≌△HCQ；

（2）若P为AB边上任意一点，延长PD到E，使DE＝PD，再以PE，PC为边作平行四边形PCQE．请问对角线PQ的长是否存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．

（3）如图2，若P为DC边上任意一点，延长PA到E，使AE＝nPA（n为常数），以PE，PB为边作平行四边形PBQE．请探究对角线PQ的长是否也存在最小值？如果存在，请求出最小值；如果不存在，请说明理由．

Answer 1

【答案】（1）见解析；（2）存在最小值，最小值为10；（3）存在最小值，最小值为 ( n＋4 )．

【解析】

（1）首先根据四边形PCQD是平行四边形，可得PD=QC；然后根据全等三角形判定的方法，判断出△APD≌△HQC即可．

（2）设与相交于点，由平行线得出，得出是上一定点，作，交的延长线于，证明，得出，求出得出，当时，的长最小，即为5．

（3）设与相交于点，由平行线得出＝＝，作，交的延长线于，过点作，交的延长线于，证明，得出＝＝，求出BH＝2(n＋1)，得出，过点作于，则四边形是矩形，得出，，证出，由三角函数得出CK＝CH·cos45°＝( 2n＋8 )＝( n＋4 )，即可得出结果．

解：（1）∵AD∥BC，

∴∠ADC＝∠DCH

即∠ADP＋∠PDC＝∠DCQ＋∠QCH，

∵四边形PCQD是平行四边形，

∴PD∥CQ，PD＝CQ，

∴∠PDC＝∠DCQ，

∴∠ADP＝∠QCH，

又∵PD＝CQ，∠A＝∠CHQ＝90°，

∴△ADP≌△HCQ（AAS）

（2）存在最小值，最小值为10．

如图，设PQ与DC相交于点G，

∵PE∥CQ，易得△DPG∽△CQG，

又PD＝DE＝PE，PE＝CQ，

∴＝ ＝ ，

∴G是DC上一定点

作QH⊥BC，交BC的延长线于H

同（1）可证∠ADP＝∠QCH

∴Rt△ADP∽Rt△QCH

∴＝ ＝，

∴CH＝4，

∴BH＝BC＋CH＝6＋4＝10，

∴当PQ⊥AB时，PQ的长最小，即为10．

（3）存在最小值，最小值为 ( n＋4 )．

如图，设PQ与AB相交于点G

∵PE∥BQ，AE＝nPA，

∴＝＝，

∴G是AB上一定点，

作QH∥DC，交CB的延长线于H，作CK⊥CD，交QH的延长线于K，

∵AD∥BC，AB⊥BC，

∴∠ADP＝∠BHQ，

∵∠PAD＋∠PAG＝∠QBH＋∠QBG＝90°，∠PAG＝∠QBG，

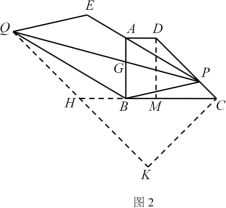
∴∠PAD＝∠QBH，

∴△ADP∽△BHQ，

∴＝＝

∴BH＝2(n＋1) ，

∴CH＝BC＋BH＝6＋2n＋2＝2n＋8，

过点D作DM⊥BC于M，则四边形ABMD是矩形，

∴BM＝AD＝2，DM＝AB＝4，

∴MC＝BC－BM＝6－2＝4＝DM，

∴∠DCM＝45°，

∴∠HCK＝45°，

∴CK＝CH·cos45°＝( 2n＋8 )＝( n＋4 ) ，

∴当PQ⊥CD时，PQ的长最小，最小值为 ( n＋4 )．