题目内容
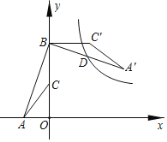
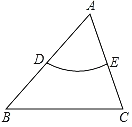
【题目】如图,在△ABC中,D,E分别是△ABC两边的中点,如果![]() (可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称
(可以是劣弧、优弧或半圆)上的所有点都在△ABC的内部或边上,则称![]() 为△ABC的中内弧,例如,图中
为△ABC的中内弧,例如,图中![]() 是△ABC其中的某一条中内弧.若在平面直角坐标系中,已知点F(0,4),O(0,0),H(4,0),在△FOH中,M,N分别是FO,FH的中点,△FOH的中内弧
是△ABC其中的某一条中内弧.若在平面直角坐标系中,已知点F(0,4),O(0,0),H(4,0),在△FOH中,M,N分别是FO,FH的中点,△FOH的中内弧![]() 所在圆的圆心P的纵坐标m的取值范围是_____.
所在圆的圆心P的纵坐标m的取值范围是_____.
【答案】m≤1或m≥2.
【解析】
先判断出点P在线段MN的垂直平分线上,再求出点M,N,Q的坐标,再分点P在MN上方和下方,即可得出得出结论.
解:如图,连接MN,

由垂径定理可知,圆心P一定在线段MN的垂直平分线上,
作MN的垂直平分线QP,
∵M,N分别是FO,FH的中点,且F(0,4),O(0,0),H(4,0),
∴M(0,2),N(2,2),Q(1,2),
若圆心在线段MN上方时,
设P(1,m)由三角形中内弧定义可知,圆心P在线段MN上方射线QP上均可,
∴m≥2,
当圆心在线段MN下方时,
∵OF=OH,∠FOH=90°
∴∠FHO=45°,
∵MN∥OH,
∴∠FNM=∠FHO=45°,
作NG⊥FH交直线QP于G,QG=NQ=1,
根据三角形中内弧的定义可知,圆心在点G的下方(含点G)的直线QP上时也符合要求;
∴m≤1,
综上所述,m≤1或m≥2,
故答案为m≤1或m≥2.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目