Question

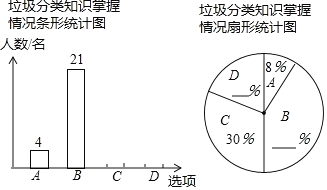
【题目】某中学为开拓学生视野，开展“课外读书周”活动，活动后期随机调查了九年级部分学生一周的课外阅读时间，并将结果绘制成两幅不完整的统计图，请你根据统计图（如图）的信息回答下列问题：

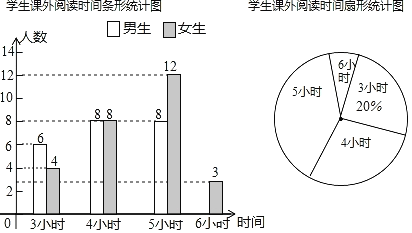
（1）本次调查的学生总数为　 　人，被调查学生的课外阅读时间的中位数是　 　小时，众数是　 　小时；

（2）请你补全条形统计图，在扇形统计图中，课外阅读时间为5小时的扇形的圆心角度数是　 　；

（3）若全校九年级共有学生700人，估计九年级一周课外阅读时间为6小时的学生有多少人？

（4）若学校需要，从二男二女四名同学中随机选取两人分享读后感，恰好是一男一女的概率？（列表或树状图）

Answer 1

【答案】（1）50；4；5；（2）144°；见解析；（3）估计九年级一周课外阅读时间为6小时的学生有56人；（4）见解析，

【解析】

（1）用阅读时间为3小数的人数除以它所占的百分比得到调查的总人数，再计算出阅读时间为6小时的男生人数，然后根据中位数、众数的定义求解；

（2）先利用阅读时间为6小时的男生人数补全条形统计图，然后用360°乘以阅读时间为5小时的人数所占的百分比得到课外阅读时间为5小时的扇形的圆心角度数；

（3）用700乘以样本中阅读时间为6小数的人数的百分比即可；

（4）画树状图展示所有12种等可能的结果数，找出恰好是一男一女的结果数，然后根据概率公式求解．

（1）（6+4）÷20%＝50，

∴本次调查的学生总数为50人，

课外阅读时间为6小时的男生人数为50﹣10﹣16﹣20﹣3＝1，

∴被调查学生的课外阅读时间的中位数是4小时，众数是5小时；

故答案为：50；4；5；

（2）课外阅读时间为5小时的扇形的圆心角度数，

补全条形统计图为：

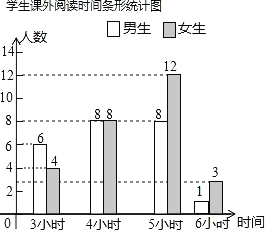
故答案为144°；

（3），

∴估计九年级一周课外阅读时间为6小时的学生有56人；

（4）画树状图为：

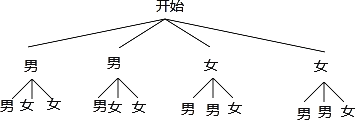
共有12种等可能的结果数，其中恰好是一男一女的结果数为8，

∴恰好是一男一女的概率．