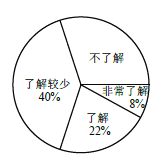
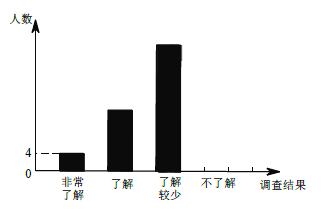
ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷ΣΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§OΈΣΉχ±ξ‘≠ΒψΘ§≈ΉΈοœΏ![]() ΫΜ
ΫΜ![]() ÷α”Ύ
÷α”Ύ![]() ΓΔ
ΓΔ![]() ΝΫΒψ(
ΝΫΒψ(![]() ‘Ύ
‘Ύ![]() ÷αΗΚΑκ÷α…œ)Θ§ΫΜ
÷αΗΚΑκ÷α…œ)Θ§ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§
Θ§![]() Θ°
Θ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œΖΫΒΎ“ΜœσœόΡΎ“ΜΒψΘ§Ν§Ϋ”
…œΖΫΒΎ“ΜœσœόΡΎ“ΜΒψΘ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§
Θ§![]() Θ§―”≥Λ
Θ§―”≥Λ![]() ΫΜ
ΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§…ηΒψ
Θ§…ηΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§«σ
Θ§«σ![]() ”κ
”κ![]() ÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ(≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩ
÷°ΦδΒΡΚ· ΐΙΊœΒ ΫΘΜ(≤Μ“Σ«σ–¥≥ωΉ‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈß)
ΒΡ»Γ÷ΒΖΕΈß)
Θ®3Θ©Α―œΏΕΈ![]() ―Ί÷±œΏ
―Ί÷±œΏ![]() Ζ≠’έΘ§ΒΟΒΫœΏΕΈ
Ζ≠’έΘ§ΒΟΒΫœΏΕΈ![]() Θ§
Θ§![]() ΈΣΒΎΕΰœσœόΡΎ“ΜΒψΘ§Ν§Ϋ”
ΈΣΒΎΕΰœσœόΡΎ“ΜΒψΘ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§
Θ§![]() Θ§
Θ§![]() ΈΣœΏΕΈ
ΈΣœΏΕΈ![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§…δœΏ
Θ§…δœΏ![]() ΫΜœΏΕΈ
ΫΜœΏΕΈ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΫΜ
ΫΜ![]() ”Ύ
”Ύ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() Θ§»τ
Θ§»τ![]() Θ§
Θ§![]() Θ§…η÷±œΏ
Θ§…η÷±œΏ![]() ”κ≈ΉΈοœΏΒΎ“ΜœσœόΫΜΒψΈΣ
”κ≈ΉΈοœΏΒΎ“ΜœσœόΫΜΒψΈΣ![]() Θ§«σΒψ
Θ§«σΒψ![]() Ήχ±ξΘ°
Ήχ±ξΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() ΘΜΘ®3Θ©
ΘΜΘ®3Θ©![]() Θ®1Θ§4Θ©
Θ®1Θ§4Θ©
ΓΨΫβΈωΓΩ
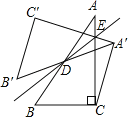
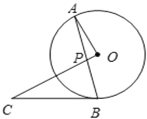
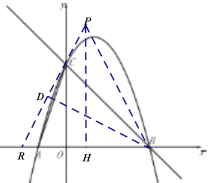
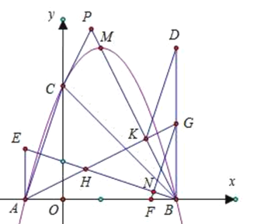
Θ®1Θ©ΗυΨί≈ΉΈοœΏΫβΈω Ϋ![]() Ω…«σΒΟΒψCΉχ±ξΘ§‘ΌΗυΨί
Ω…«σΒΟΒψCΉχ±ξΘ§‘ΌΗυΨί![]() Θ§Ω…«σΒΟΒψAΉχ±ξΘ§‘ΌΫΪΒψAΉχ±ξ¥ζ»κΫβΈω ΫΦ¥Ω…«σΒΟΘΜ
Θ§Ω…«σΒΟΒψAΉχ±ξΘ§‘ΌΫΪΒψAΉχ±ξ¥ζ»κΫβΈω ΫΦ¥Ω…«σΒΟΘΜ
Θ®2Θ©»γΆΦΘ§ΙΐΒψPΉςPHΓΆx÷α”ΎHΘ§ΙΐΒψBΉςBDΓΆPRΘ§÷ΛΟςΓœPRB=ΓœPBRΘ§‘ρΓςPRBΈΣΒ»―ϋ»ΐΫ«–ΈΘ§Φ¥Ω…ΒΟΒΫRH=HBΘ§‘Ό¥ζ»κΗςΒψΚαΉχ±ξΦ¥Ω…«σΒΟΙΊœΒ ΫΘΜ
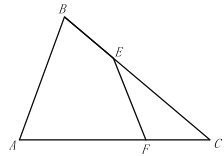
Θ®3Θ©»γΆΦΘ§…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§‘ρEΘ®©¹1Θ§
Θ§‘ρEΘ®©¹1Θ§![]() Θ©Θ§
Θ©Θ§
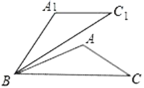
”…![]() Θ§«“BDΈΣœΏΕΈAB―Ί÷±œΏBCΖ≠’έΥυΒΟΘ§Ω…÷ΣΒψDΘ®3Θ§4Θ©Θ§«σΒΟ
Θ§«“BDΈΣœΏΕΈAB―Ί÷±œΏBCΖ≠’έΥυΒΟΘ§Ω…÷ΣΒψDΘ®3Θ§4Θ©Θ§«σΒΟ![]() Θ§
Θ§
”…FNΓΆBE÷Σ![]() Θ§‘ρ
Θ§‘ρ![]() Θ§Ω…«σ÷±œΏFGΒΡΫβΈω ΫΈΣΘΚ
Θ§Ω…«σ÷±œΏFGΒΡΫβΈω ΫΈΣΘΚ![]() Θ§ΫχΕχ«σΒΟ
Θ§ΫχΕχ«σΒΟ![]() Θ§“ρΈΣ
Θ§“ρΈΣ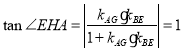 Θ§¥ζ»κΩ…«σΒΟ
Θ§¥ζ»κΩ…«σΒΟ![]() Θ§‘ρΒψGΉχ±ξΈΣΘ®3Θ§2Θ©Θ§Υυ“‘÷±œΏAGΒΡΫβΈω ΫΈΣΘΚ
Θ§‘ρΒψGΉχ±ξΈΣΘ®3Θ§2Θ©Θ§Υυ“‘÷±œΏAGΒΡΫβΈω ΫΈΣΘΚ![]() Θ§÷±œΏBEΒΡΫβΈω ΫΈΣΘΚ
Θ§÷±œΏBEΒΡΫβΈω ΫΈΣΘΚ![]() ΘΜ‘Ό…ηΒψKΘ®uΘ§
ΘΜ‘Ό…ηΒψKΘ®uΘ§![]() Θ©Θ§‘ρ
Θ©Θ§‘ρ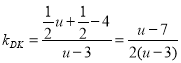 Θ§
Θ§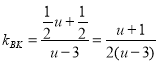 Θ§”…
Θ§”…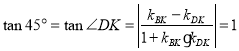 Θ§ΫβΒΟ
Θ§ΫβΒΟ![]() Θ§‘ρKΘ®
Θ§‘ρKΘ®![]() Θ§
Θ§![]() Θ©Θ§÷±œΏBKΒΡΫβΈω ΫΈΣΘΚ
Θ©Θ§÷±œΏBKΒΡΫβΈω ΫΈΣΘΚ![]() Θ§”…ΒψMΈΣ÷±œΏBK”κ≈ΉΈοœΏΒΡΫΜΒψΘ§ΝΣΝΔΖΫ≥ΧΦ¥Ω…«σΒΟΒψMΘ®1Θ§4Θ©Θ°
Θ§”…ΒψMΈΣ÷±œΏBK”κ≈ΉΈοœΏΒΡΫΜΒψΘ§ΝΣΝΔΖΫ≥ΧΦ¥Ω…«σΒΟΒψMΘ®1Θ§4Θ©Θ°
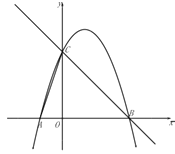
ΫβΘΚΘ®1Θ©”…≈ΉΈοœΏ![]() Ω…÷ΣΘ§
Ω…÷ΣΘ§
ΒψCΘ®0Θ§3Θ©Θ§
ΓύOC=3Θ§
ΓΏ![]() Θ§
Θ§
ΓύOA=1Θ§
ΓύAΘ®©¹1Θ§0Θ©Θ§
ΫΪΒψAΘ®©¹1Θ§0Θ©¥ζ»κ![]() Θ§
Θ§
Ω…«σΒΟΘΚb=2Θ§
Γύ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚ![]()
Θ®2Θ©»γΆΦΘ§ΙΐΒψPΉςPHΓΆx÷α”ΎHΘ§ΙΐΒψBΉςBDΓΆPRΘ§
”…Θ®1Θ©÷Σ≈ΉΈοœΏΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
ΓύΩ…«σΒΟΒψBΉχ±ξΈΣΘ§Θ®3Θ§0Θ©Θ§
ΓύOC=OBΘ§
ΓύΓœCBO=45ΓψΘ§
ΓΏ![]() Θ§
Θ§
ΓύΓœPBC=ΓœDBCΘ§
ΓΏΓœPBR=ΓœPBCΘΪΓœCBO=45ΓψΘΪΓœPBCΘ§ΓœDRB=90ΓψΘ≠ΓœDBRΘ§ΕχΓœDBR=ΓœCBOΘ≠ΓœDBOΘ§
ΓύΓœDRB=90ΓψΘ≠ΓœCBO+ΓœDBO=45ΓψΘΪΓœDBOΘ§
ΓύΓœPRB=ΓœPBRΘ§
ΓύΓςPRBΈΣΒ»―ϋ»ΐΫ«–ΈΘ§RH=HBΘ§
ΓΏΒψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§Βψ
Θ§Βψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]()
Γύ![]() Θ§
Θ§
Φ¥![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΘ§
…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
ΓύEΘ®©¹1Θ§![]() Θ©Θ§
Θ©Θ§
ΓΏ![]() Θ§BDΈΣœΏΕΈAB―Ί÷±œΏBCΖ≠’έΥυΒΟΘ§
Θ§BDΈΣœΏΕΈAB―Ί÷±œΏBCΖ≠’έΥυΒΟΘ§
ΓύΒψDΘ®3Θ§4Θ©Θ§
Γύ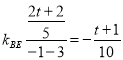 Θ§
Θ§
ÿFNâBEȧ
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ÷±œΏFGΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
Νν![]() Θ§‘ρ
Θ§‘ρ![]() Θ®3Θ§
Θ®3Θ§![]() Θ©Θ§
Θ©Θ§
Γύ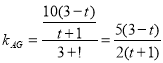
ΓΏΓœEHA=45ΓψΘ§
”…÷±œΏΒΡΦ–Ϋ«ΙΪ ΫΒΟΘΚ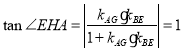 Θ§
Θ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Μ·ΦρΒΟΘΚ![]() Θ§
Θ§
Φ¥![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύGΘ®3Θ§2Θ©Θ§
Γύ÷±œΏAGΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
Γύ÷±œΏBEΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
…ηΒψKΘ®uΘ§![]() Θ©Θ§
Θ©Θ§![]() Θ§
Θ§
Γύ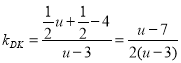 Θ§
Θ§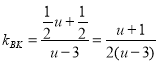 Θ§
Θ§
”…÷±œΏΦ–Ϋ«ΙΪ ΫΒΟΘΚ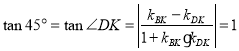 ,
,
Φ¥Θ§![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
Μ·ΦρΒΟΘΚ![]() Μρ
Μρ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§
ΓΏ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύKΘ®![]() Θ§
Θ§![]() Θ©Θ§
Θ©Θ§
Γύ÷±œΏBKΒΡΫβΈω ΫΈΣΘΚ![]() Θ§
Θ§
ΓΏΒψMΈΣ÷±œΏBK”κ≈ΉΈοœΏΒΡΫΜΒψΘ§
ΓύΝΣΝΔ![]() Θ§
Θ§
ΫβΒΟΘΚ![]() Μρ
Μρ![]() Θ®Φ¥ΈΣΒψBΘ§…α»ΞΘ©Θ§
Θ®Φ¥ΈΣΒψBΘ§…α»ΞΘ©Θ§
Υυ“‘ΒψMΘ®1Θ§4Θ©Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ