题目内容
【题目】观察下列各式：
13＝
×12×22
13+23＝9＝×22×32
13+23+33＝36＝×32×42
13+23+33+43＝100＝×42×52
回答下面的问题：
(1)猜想：13+23+33+…+(n－1)3+ n3＝________.
(2)利用你得到的(1)中的结论，计算13+23+33+…+993+1003的值.
(3)计算：213+223+…+993+1003的值.
【答案】（1）
n2(n+1)2(2) 25502500；(3) 25458400.
【解析】
（1）（2）观察已知的等式，发现：等式的左边是连续自然数的立方和，等式的右边是连续自然数的和的平方；由此得出答案即可；
（3）根据（1）中发现的结论，即可求得结论．
(1)∵13＝×12×22
13+23＝9＝×22×32
13+23+33＝36＝×32×42
13+23+33+43＝100＝×42×52
…
∴猜想：13+23+33+…+(n－1)3+ n3＝n2(n+1)2；
故填：n2(n+1)2
(2) 13+23+33+…+993+1003=×1002×1012=25502500；
(3) 213+223+…+993+1003
=13+23+33+…+993+1003(13+23+33+43+…203)
= ×1002×1012×202×212
=25458400.
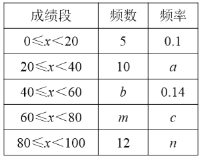
【题目】某校为更好的开展“春季趣味运动会”活动，随机在各年级抽查了部分学生，了解他们最喜爱的趣味运动项目类型（跳绳、实心球、50m、拔河共四类），并将统计结果绘制成如下不完整的频数分布表（如图所示）
根据以上信息回答下列问题：
最喜爱的趣味运动项目类型频数分布表：
项目类型 | 频数 | 频率 |
跳绳 | 25 | a |
实心球 | 20 |
|
50m | b | 0.4 |
拔河 | 0.15 |
（1）直接写出a= ，b= ；
（2）将图中的扇形统计图补充完整（注明项目、百分比）；
（3）若全校共有学生1200名，估计该校最喜爱50m和拔河的学生共约有多少人？
【题目】从2012年7月1日起某市执行新版居民阶梯电价，小明同学家收到了新政后的第一张电费单，小明爸爸说：“小明，请你计算一下，这个月的电费支出与新政前相比是多了还是少了？”于是小明上网了解了有关电费的收费情况，得到如下两表：
2004年1月至2012年6月执行的收费标准：
月用电量（度）50度有以下部分 | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
单价（元/度） | 0.53 | 0.56 | 0.63 |
2012年7月起执行的收费标准：
月用电量（度） | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
单价（元/度） | 0.53 | 0.58 | 0.83 |
（1）若小明家2012年7月份的用电量为200度，则小明家7月份的电费支出是多少元?比新政前少了多少元?
（2）若新政后小明家的月用电量为a度，请你用含a的代数式表示当月的电费支出．
