��Ŀ����
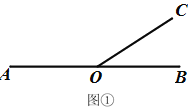
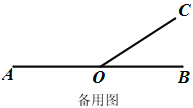
����Ŀ����֪����ͼ1����O��ֱ��AB��һ�㣬����O������OC.
(1)����AOC=140�������BOC=________��.
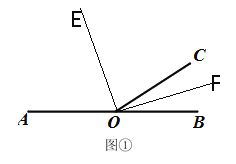
(2)��ͼ1�зֱ�AOC�Ľ�ƽ����OE�͡�BOC�Ľ�ƽ����OF����ô,OE��OF��ʲôλ�ù�ϵ����˵������.
(3)����BOC=30��������OD��OB�������Ƶ�O��ÿ��10���ǵ��ٶ���ʱ����ת.������OD������OA�غ�ʱ������OC��ÿ��30���ǵ��ٶ��Ƶ�O��ʱ����ת������OD��ԭ�����ٶȺͷ��������ת��������OC������OD����һ������������OB�غ�ʱ���������߶�ֹͣ.������OD��ת��ʱ��Ϊt�룬����ת�Ĺ����У��Ƿ����ij��ʱ�̣�ʹ������OB��OC��OD�е�ijһ���������������������нǵ�ƽ����?�����ڣ�ֱ��д����������������t��ֵ���������ڣ�˵������.
���𰸡���1��40����2��EO��FO�����ɼ�������3��t=1.5s��6s
��������
��1�������ڲ��Ǽ�����⣻
��2�����ݽ�ƽ�����봹ֱ�Ķ��弴����⣻
��3��������OD������OB������OC�Ľ�ƽ���ߣ�����OC������OD������OB�Ľ�ƽ���ߣ�����OB������OD������OC�Ľ�ƽ���߷ֱ����ۼ������.
��1���ߡ�AOC=140�������BOC=180��-��AOC=40����
���40��
��2��EO��FO���������£�
��ͼ����OE����AOC�Ľ�ƽ���ߣ�OF����BOC�Ľ�ƽ���ߣ�
���COE=![]() ��AOC����COF=
��AOC����COF=![]() ��BOC��
��BOC��
����COE+��COF=![]() ��AOC+
��AOC+![]() ��BOC=
��BOC=![]() (��AOC+��BOC)=
(��AOC+��BOC)=![]() ��180��=90����
��180��=90����
����EOF=90�㣬
��EO��FO.
��3��������õ�OD�˶���OAʱ��t=18s����OD�˶���OBʱ��t=36s,��OC�˶���OBʱ��t=18+330��30=29s,
������OD������OB������OC�Ľ�ƽ����ʱ��
��OD�˶���OC����ʱ��0��t��18��
����BOC=30����
���BOD=![]() ��BOC=15�㣬
��BOC=15�㣬
��t=15��10=1.5s
��OD�˶���OCҲ�˶�ʱ��18��t��29,
��BOD=360��-10t,��BOC=360��-30-30��t-18��
�ߡ�BOD=![]() ��BOC
��BOC
��360��-10t=![]() [360��-30-30��t-18��]
[360��-30-30��t-18��]
���t=15s,���������⣬��ȥ��
������OC������OD������OB�Ľ�ƽ����ʱ
��OD�˶���OC����ʱ��0��t��18��
����BOC=30�㣬
����BOD=2��BOC=60����t=60��10=6s;
��OD�˶���OCҲ�˶�ʱ��18��t��29,
����OC������OB������OD���ж۽�֮�䣬���������⣻
������OB������OD������OC�Ľ�ƽ����
�����ڵ�OD�˶���OC�����������
��OD�˶���OCҲ�˶�ʱ��18��t��29,
����OB������OC������OD���ж۽�֮�䣬����������
���ϣ�t=1.5s��6sʱ��ʹ������OB��OC��OD�е�ijһ���������������������нǵ�ƽ����.

����Ŀ������ͼ����һ��������ֽƬ�������ĸ���С��״һ����С�����Σ�Ȼ�����е�һ��С�������ٰ�ͬ���ķ��������ĸ�С�����Σ��ٽ����е�һ��С�����μ����ĸ�С�����Σ����ѭ����ȥ��
��1��������
���Ĵ��� | 1 | 2 | 3 | 4 | 5 |
������� | 4 | 7 | 10 | �� �� | �� �� |
��2���������8�Σ��������� ����С�����Σ�
��3�������n�Σ��������� ����С�����Σ�
��4�������������ֽƬΪ1�����n�κ���С�����εı߳�Ϊ�� ����



