Question

【题目】如图，已知⊙O的半径为5，直线l切⊙O于A，在直线l上取点B，AB=4．

（1）请用无刻度的直尺和圆规，过点B作直线m⊥l，交⊙O于C、D（点D在点C的上方）；（保留作图痕迹，不要求写作法）

（2）求BC的长．

Answer 1

【答案】（1）答案见解析；（2）2．

【解析】试题分析：（1）利用基本作图（过一点作已知直线的垂线）作直线m得到CD；

（2）作OH⊥CD于H，连接OA、OD，如图，利用垂径定理得到DH=CH，则根据切线的性质得OA⊥l，易得四边形OABH为正方形，所以OH=AB=4，BH=OA=5，然后利用勾股定理计算出DH=3，则CH=3，所以BC=BH﹣CH=2．

试题解析：解：（1）如图，CD为所作；

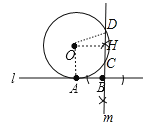
（2）作OH⊥CD于H，连接OA、OD，如图，则DH=CH．∵直线l切⊙O于A，∴OA⊥l，易得四边形OABH为正方形，∴OH=AB=4，BH=OA=5．在Rt△ODH中，DH==3，∴CH=3，∴BC=BH﹣CH=5﹣3=2．