题目内容
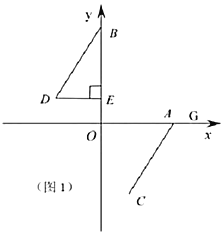
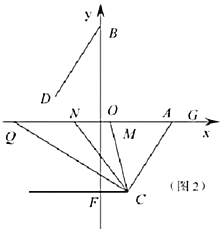
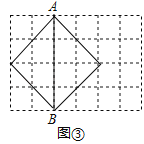
【题目】定义:若以一条线段为对角线作正方形,则称该正方形为这条线段的“对角线正方形”.例如,图①中正方形ABCD即为线段BD的“对角线正方形”.如图②,在△ABC中,∠ABC=90°,AB=3cm,BC=4cm,点P从点C出发,沿折线CA﹣AB以5cm/s的速度运动,当点P与点B不重合时,作线段PB的“对角线正方形”,设点P的运动时间为t(s),线段PB的“对角线正方形”的面积为S(cm2).
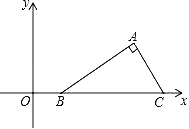
(1)如图③,借助虚线的小正方形网格,画出线段AB的“对角线正方形”.
(2)当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,求t的值.
(3)当点P沿折线CA﹣AB运动时,求S与t之间的函数关系式.
(4)在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠A的平分线上时,直接写出t的值.



【答案】(1)见解析;(2)![]() ;(3)S=
;(3)S=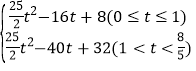 ;
;
(4)t的值为![]() s 或1s或
s 或1s或![]() s
s
【解析】试题分析:(1)t=0时,正方形的对角线为4,由此即可求出面积.
(2)如图1中,当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,设正方形的边长为x,由PE∥AB,可得 ![]() =
=![]() =
=![]() ,解得x=
,解得x=![]() ,再求出PC的长即可解决问题.
,再求出PC的长即可解决问题.
(3)分两种情形分别求解①如图2中,当0≤t≤1时,作PH⊥BC于H.求出PB2即可.②如图3中,当1<t<![]() 时,求出PB2即可.
时,求出PB2即可.
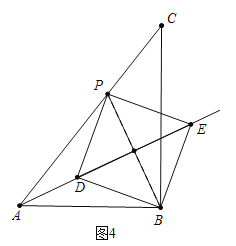
(4)分三种情形讨论①如图4中,当D、E在∠BAC的平分线上时.②当点P运动到点A时,满足条件,此时t=1s.③如图5中,当点E在∠BAC的角平分线上时,分别求解即可.
试题解析:解:(1)线段AB的“对角线正方形”如图所示:
(2)如图1中,当线段PB的“对角线正方形”有两边同时落在△ABC的边上时,设正方形的边长为x.∵PE∥AB,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,解得x=
,解得x=![]() ,∴PE=
,∴PE=![]() ,CE=4﹣
,CE=4﹣![]() =
=![]() ,∴PC=
,∴PC=![]() =
=![]() ,∴t=
,∴t=![]() =
=![]() s;
s;

(3)①如图2中,当0≤t≤1时,作PH⊥BC于H.
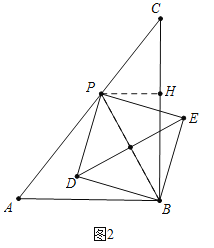
∵PC=5t,则HC=4t,PH=3t.在Rt△PHB中,PB2=PH2+BH2=(3t)2+(4﹣4t)2=25t2﹣32t+16,∴S=![]() PB2=
PB2=![]() t2﹣16t+8.
t2﹣16t+8.
②如图3中,当1<t<![]() 时,∵PB=8﹣5t,∴S=
时,∵PB=8﹣5t,∴S=![]() PB2=
PB2=![]() t2﹣40t+32.
t2﹣40t+32.
综上所述:S=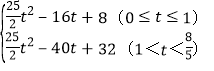 ;
;
(4)①如图4中,当D、E在∠BAC的平分线上时,易知AB=AP=3,PC=2,∴t=![]() s.
s.
②当点P运动到点A时,满足条件,此时t=1s.
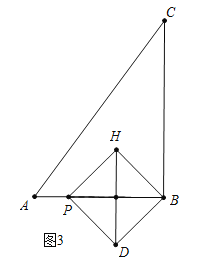
③如图5中,当点E在∠BAC的角平分线上时,作EH⊥BC于H.
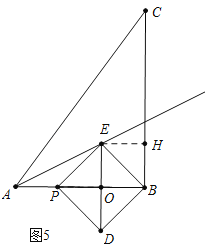
易知EB平分∠ABC,∴点E是△ABC的内心,四边形EOBH是正方形,OB=EH=EO=BH=![]() =1(直角三角形内切圆半径公式),∴PB=2OB=2,∴AP=1,∴t=
=1(直角三角形内切圆半径公式),∴PB=2OB=2,∴AP=1,∴t=![]() s.综上所述:在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠CAB的平分线上时,t的值为
s.综上所述:在整个运动过程中,当线段PB的“对角线正方形”至少有一个顶点落在∠CAB的平分线上时,t的值为 ![]() s 或1s或
s 或1s或 ![]() s;
s;

 阅读快车系列答案
阅读快车系列答案