题目内容
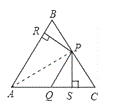
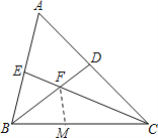
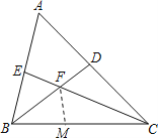
【题目】在△ABC中,∠A=60°,BD,CE是△ABC的两条角平分线,且BD,CE交于点F,如图所示,用等式表示BE,BC,CD这三条线段之间的数量关系,并证明你的结论;
晓东通过观察,实验,提出猜想:BE+CD=BC,他发现先在BC上截取BM,使BM=BE,连接FM,再利用三角形全等的判定和性质证明CM=CD即可.
(1)下面是小东证明该猜想的部分思路,请补充完整;
①在BC上截取BM,使BM=BE,连接FM,则可以证明△BEF与______全等,判定它们全等的依据是______;
②由∠A=60°,BD,CE是△ABC的两条角平分线,可以得出∠EFB=______°;
(2)请直接利用①,②已得到的结论,完成证明猜想BE+CD=BC的过程.
【答案】(1)①△BMF,SAS;②60;(2)见解析
【解析】
(1)①由BD,CE是△ABC的两条角平分线知∠FBE=∠FBC=![]() ∠ABC,结合BE=BM,BF=BF,依据“SAS”即可证得△BEF≌△BMF;
∠ABC,结合BE=BM,BF=BF,依据“SAS”即可证得△BEF≌△BMF;
②利用三角形内角和求出∠ABC+∠ACB=120°,进而得出∠FBC+∠FCB=60°,得出∠BFC=120°,即可得出结论;
(2)利用角平分线得出∠EBF=∠MBF,进而得出△BEF≌△BMF,求出∠BFM,即可判断出∠CFM=∠CFD,即可判断出△FCM≌△FCD,即可得出结论.
(1)解:①在BC上取一点M,使BM=BE,连接FM,如图所示:
∵BD、CE是△ABC的两条角平分线,
∴∠FBE=∠FBM=![]() ∠ABC,
∠ABC,
在△BEF和△BMF中,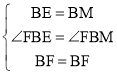 ,
,
∴△BEF≌△BMF(SAS),
故答案为:△BMF,SAS;
②∵BD、CE是△ABC的两条角平分线,
∴∠FBC+FCB=![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
在△ABC中,∠A+∠ABC+∠ACB=180°,
∵∠A=60°,
∴∠ABC+∠ACB=180°-∠A=180°-60°=120°,
∴∠BFC=180°-(∠FBC+∠FCB)=180°-![]() (∠ABC+∠ACB)=180°-
(∠ABC+∠ACB)=180°-![]() ×120°=120°,
×120°=120°,
∴∠EFB=60°,
故答案为:60;
(2)证明:由①知,∠BFE=60°,
∴∠CFD=∠BFE=60°
∵△BEF≌△BMF,
∴∠BFE=∠BFM=60°,
∴∠CFM=∠BFC-∠BFM=120°-60°=60°,
∴∠CFM=∠CFD=60°,
∵CE是∠ACB的平分线,
∴∠FCM=∠FCD,
在△FCM和△FCD中,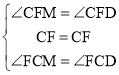 ,
,
∴△FCM≌△FCD(ASA),
∴CM=CD,
∴BC=CM+BM=CD+BE,
∴BE+CD=BC.

 阅读快车系列答案
阅读快车系列答案