题目内容
【题目】探究下面的问题:
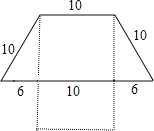
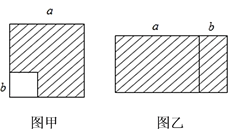
(1)如图甲,在边长为a的正方形中去掉一个边长为b的小正方形(a>b),把余下的部分剪拼成如图乙的一个长方形,通过计算两个图形(阴影部分)的面积,验证了一个等式,这个等式是________(用式子表示),即乘法公式中的___________公式.
(2)运用你所得到的公式计算:
①10.7×9.3
②![]()
【答案】(1)a2-b2=(a+b)(a-b);平方差;(2)①99.51;②x2-6xz+9z2-4y2.
【解析】
(1)这个图形变换可以用来证明平方差公式:已知在左图中,大正方形减小正方形剩下的部分面积为a2-b2;因为拼成的长方形的长为(a+b),宽为(a-b),根据“长方形的面积=长×宽”代入为:(a+b)×(a-b),因为面积相等,进而得出结论.
(2)①将10.7×9.3化为(10+0.7)×(10-0.7),再用平方差公式求解即可.
②利用平方差公式和完全平方公式求解即可.
(1) 由图知:大正方形减小正方形剩下的部分面积为a2-b2;
拼成的长方形的面积:(a+b)×(ab),所以得出:a2-b2=(a+b)(ab);
故答案为:a2-b2=(a+b)(ab);平方差
(2)①原式=(10+0.7)×(10-0.7)
=102-0.72
=100-0.49
=99.51.
②原式=(x-3z+2y)(x-3z-2y)
=(x-3z)2-(2y)2
=x2-6xz+9z2-4y2.

 小学期末标准试卷系列答案
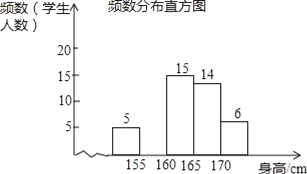
小学期末标准试卷系列答案【题目】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查,利用所得数据绘成如图统计图表:
频数分布表
身高分组 | 频数 | 百分比 |
x<155 | 5 | 10% |
155≤x<160 | a | 20% |
160≤x<165 | 15 | 30% |
165≤x<170 | 14 | b |
x≥170 | 6 | 12% |
总计 | 100% |
(1)填空:a=____,b=____;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,估计身高不低于165cm的学生大约有多少人?