题目内容
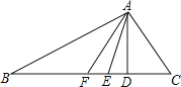
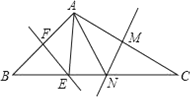
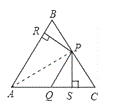
【题目】如图,在△ABC中,点P、Q分别是BC、AC边上的点,PS![]() AC,PR
AC,PR![]() AB,若
AB,若![]() ,PR
,PR![]() PS,则下列结论:①PA平分
PS,则下列结论:①PA平分![]() ,②AS
,②AS![]() AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
AR;③QP∥AR;④△BRP≌△CPS;其中正确的结论有( )
A. 4个B. 3个C. 2个D. 1个
【答案】B
【解析】
根据角平分线判定定理即可推出①,根据勾股定理即可推出②AR=AS,根据等腰三角形性质推出∠QAP=∠QPA,推出∠QPA=∠BAP,根据平行线判定推出③QP∥AB即可;无法证明△BRP≌△CSP故④错误.
∵PR⊥AB,PS⊥AC,PR=PS,
∴点P在∠A的平分线上,故①正确,
∠ARP=∠ASP=90°,
∴∠SAP=∠RAP,
在Rt△ARP和Rt△ASP中,由勾股定理得:AR2=AP2-PR2,AS2=AP2-PS2,
∵AP=AP,PR=PS,
∴AR=AS,∴②正确;
∵AQ=QP,
∴∠QAP=∠QPA,
∵∠QAP=∠BAP,
∴∠QPA=∠BAP,
∴QP∥AR,∴③正确;
在△BRP和△CSP中,缺少全等条件,故④错误,
故选B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目