题目内容
【题目】如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0)、B(0,4),点D在y轴的负半轴上,若将△DAB沿直线AD折叠,点B恰好落在x轴正半轴上的点C处.
(1)求直线AB的表达式;
(2)求点C和点D的坐标;
(3)y轴的正半轴上是否存在一点P,使得S△PAB=![]() S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
S△OCD?若存在,求出点P的坐标;若不存在,请说明理由.
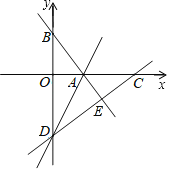
【答案】(1)y=﹣![]() x+4;(2)C(8,0),D(0,-6);(3)存在,P(0,8)
x+4;(2)C(8,0),D(0,-6);(3)存在,P(0,8)
【解析】
(1)将点A、B的坐标代入一次函数表达式:y=kx+b,即可求解;
(2)由题意得:AD=AB=5,故点D(8,0),设点C的坐标为:(0,m),而CD=BC,即4﹣m=![]() ,再解答即可;
,再解答即可;
(3)设点P(0,n),![]() S△OCD=
S△OCD=![]() =
=![]() ×6×8=6,S△ABP=
×6×8=6,S△ABP=![]() BP×xA=
BP×xA=![]() |4﹣m|×3=6,即可求解.
|4﹣m|×3=6,即可求解.
解:(1)设直线AB的表达式为:y=kx+b
将点A、B的坐标代入一次函数表达式:y=kx+b
得:![]() ,解得:
,解得: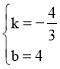 ,
,
故直线AB的表达式为:y=﹣![]() x+4;
x+4;
(2)∵AB=![]()
由折叠可得:AC=AB=5,故点C(8,0),
设点D的坐标为:(0,m),而CD=BC,
即4﹣m=![]() ,解得:m=﹣6,
,解得:m=﹣6,
故点D(0,﹣6);
(3)设点P(0,n),
∵![]() S△OCD=
S△OCD=![]() =
=![]() ×6×8=6,
×6×8=6,
∴S△ABP=![]() BP×xA=
BP×xA=![]() |4﹣n|×3=6,
|4﹣n|×3=6,
解得:n=8或0,
又∵点P在y轴的正半轴,
∴n=8,
故P(0,8).

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目