题目内容
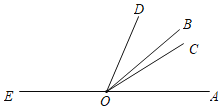
【题目】如图,点O是直线AE上的一点,OC是∠AOD的平分线,∠BOD=![]() ∠AOD.
∠AOD.
(1)若∠BOD=20°,求∠BOC的度数;
(2)若∠BOC=n°,用含有n的代数式表示∠EOD的大小.
【答案】(1)10°;(2)180°﹣6n
【解析】
(1)根据∠BOD=![]() ∠AOD.∠BOD=20°,可求出∠AOD,进而求出答案;
∠AOD.∠BOD=20°,可求出∠AOD,进而求出答案;
(2)设∠BOD的度数,表示∠AOD,用含有n的代数式表示∠AOD,从而表示∠DOE.
解:(1)∵∠BOD=![]() ∠AOD.∠BOD=20°,
∠AOD.∠BOD=20°,
∴∠AOD=20°×3=60°,
∵OC是∠AOD的平分线,
∴∠AOC=∠COD=![]() ∠AOD=
∠AOD=![]() ×60°=30°,
×60°=30°,
∴∠BOC=∠COD﹣∠BOD=30°﹣20°=10°;
(2)设∠BOD=x,则∠AOD=3x,
有(1)得,∠BOC=∠COD﹣∠BOD,
即:n=![]() x﹣x,解得:x=2n,
x﹣x,解得:x=2n,
∴∠AOD=3∠BOD=6n,
∠EOD=180°﹣∠AOD=180°﹣6n,

练习册系列答案
相关题目
【题目】某班对道德与法治,历史,地理三门程的选考情况进行调研,数据如下:
科目 | 道德与法治 | 历史 | 地理 |
选考人数(人) | 19 | 13 | 18 |
其中道德与法治,历史两门课程都选了的有3人,历史,地理两门课程都选了的有4人,该班至多有多少学生( )
A.41B.42C.43D.44