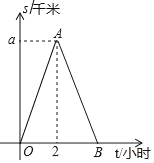
��Ŀ����
����Ŀ��С���Ӽҳ����ر���·����̲��ͽ������������̲����������ԭ·���أ�С���뿪�ҵ�·��s����λ��ǧ�ף����߲�ʱ��t����λ��Сʱ��֮��ĺ�����ϵ��ͼ��ʾ�����дӼҵ���̲����ƽ���ٶ���4ǧ��/ʱ������ͼ���ṩ����Ϣ������������⣺
��1����ͼ�е�aֵ��
��2�����ھ���С����5ǧ�״���һ���ص�C��С���ӵ�һ�㾭����C���ڶ��㾭����C������ʱ��Ϊ1.75Сʱ����С�����ع����У�s��t�ĺ�������ʽ������д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£���С���ӳ������ص������õ�ʱ�䣮
���𰸡���1��8����2��s=��3t+14����3��С���ӳ������ص������õ�ʱ����![]() Сʱ��
Сʱ��
������������: ��1������·��=�ٶ���ʱ�伴�����aֵ��
��2�������ٶ�=·����ʱ��������˷���ʱ���ٶȣ��ٸ���·��=8-����ʱ���ٶ���ʱ�伴�ɵó�AB����ֱ�ߵĺ�������ʽ��
��3������2���еĺ�����ϵʽ��s=0�����tֵ���ɣ�
���:
��1��������ɵã�
a=2��4=8��
��a��ֵ��8��
��2��������ɵã�
С���Ӽҵ����Ĺ����У�C�㵽A���õ�ʱ��Ϊ����8��5����4=0.75Сʱ��
С���ӹ����ҵĹ����У�A�㵽C���õ�ʱ��Ϊ1.75��0.75=1Сʱ���ٶ�Ϊ����8��5����1=3ǧ��/ʱ��
��С���ӹ������õ�ʱ��Ϊ��8��3=![]() Сʱ��
Сʱ��
���A��2��8������B��![]() ��0��
��0��
��С�����ع����У�s��t�ĺ�������ʽ��s=kt+b��
 ����
����![]()
��С�����ع����У�s��t�ĺ�������ʽ��s=��3t+14��
��3����s=0ʱ����3t+14=0����t=![]() ��
��
��С���ӳ������ص������õ�ʱ����![]() Сʱ��
Сʱ��
�㾦: ���⿼��һ�κ�����Ӧ�ã������Ĺؼ�����ȷ���⣬�����Ӧ�ĺ�������ʽ�����ú�����˼������ν�ϵ�˼����

����Ŀ����֪һԲ������ı�ֱ����![]() �������涨ֱ�����ȵ�����(����)��������������涨ֱ�����ȵ�����(����)��������������Աij�γ���������Ʒ�����Ľ�����£�
�������涨ֱ�����ȵ�����(����)��������������涨ֱ�����ȵ�����(����)��������������Աij�γ���������Ʒ�����Ľ�����£�
��� |
|
|
|
|
|
ֱ������/ |
|
|
|
|
|
��1����ָ���ļ���Ʒ�Ĵ�С�����Ҫ��
��2������涨���ľ���ֵ��![]() ֮������Ʒ.���ľ���ֵ��
֮������Ʒ.���ľ���ֵ��![]() ֮���Ǵ�Ʒ�����ľ���ֵ����
֮���Ǵ�Ʒ�����ľ���ֵ����![]() ���Ƿ�Ʒ����ô���������Ʒ�У���Щ����Ʒ����Щ�Ǵ�Ʒ����Щ�Ƿ�Ʒ��
���Ƿ�Ʒ����ô���������Ʒ�У���Щ����Ʒ����Щ�Ǵ�Ʒ����Щ�Ƿ�Ʒ��