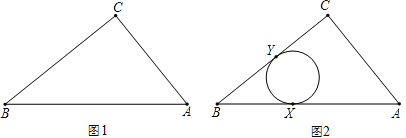题目内容
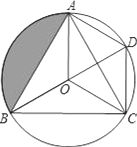
【题目】如图1,在平面直角坐标系中,矩形OABC如图所示放置,点A在x轴上,点B的坐标为(n,1)(n>0),将此矩形绕O点逆时针旋转90°得到矩形OA′B′C′,抛物线y=ax2+bx+c(a≠0)经过A、A′、C′三点.
(1)求此抛物线的解析式(a、b、c可用含n的式子表示);
(2)若抛物线对称轴是x=1的一条直线,直线y=kx+2(k≠0)与抛物线相交于两点D(x1,y1)、E(x2、y2)(x1<x2),当|x1﹣x2|最小时,求抛物线与直线的交点D和E的坐标;
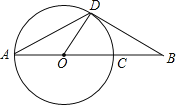
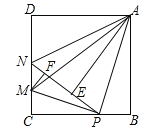
(3)若抛物线对称轴是x=1的一条直线,如图2,点M是抛物线的顶点,点P是y轴上一动点,点Q是坐标平面内一点,四边形APQM是以PM为对角线的平行四边形,点Q′与点Q关于直线CM对称,连接MQ′、PQ′,当△PMQ′与平行四边形APQM重合部分的面积是平行四边形的面积的![]() 时,求平行四边形APQM的面积.
时,求平行四边形APQM的面积.

【答案】(1)y=﹣x2+(n﹣1)x+n;(2)D(﹣1,0),E(1,4);(3)5或10.
【解析】
(1)先根据四边形ABCD是矩形,点B的坐标为(n,1)(n>0),求出点A、C的坐标,再根据图形旋转的性质求出A′、C′的坐标;把A、A′、C′三点的坐标代入即可得出a、b、c的值,进而得出其抛物线的解析式;
(2)将一次函数与二次函数组成方程组,得到一元二次方程x2+(k-2)x-1=0,根据根与系数的关系求出k的值,进而求出D(-1,0),E(1,4);
(3)设P(0,p),根据平行四边形性质及点M坐标可得Q(2,4+p),分P点在AM下方与P点在AM上方两种情况,根据重合部分的面积关系及对称性求得点P的坐标后即可得APQM面积.
解:(1)∵四边形ABCO是矩形,点B的坐标为(n,1)(n>0),
∴A(n,0),C(0,1),
∵矩形OA′B′C′由矩形OABC旋转而成,
∴A′(0,n),C′(﹣1,0);
将抛物线解析式为y=ax2+bx+c,
∵A(n,0),A′(0,n),C′(﹣1,0),
∴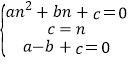 ,
,
解得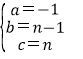 ,
,
∴此抛物线的解析式为:y=﹣x2+(n﹣1)x+n;
(2)对称轴为x=1,得﹣![]() =1,解得n=3,
=1,解得n=3,
则抛物线的解析式为y=﹣x2+2x+3.
由![]() ,
,
整理可得x2+(k﹣2)x﹣1=0,
∴x1+x2=﹣(k﹣2),x1x2=﹣1.
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(k﹣2)2+4.
∴当k=2时,(x1﹣x2)2的最小值为4,即|x1﹣x2|的最小值为2,
∴x2﹣1=0,由x1<x2可得x1=﹣1,x2=1,即y1=4,y2=0.
∴当|x1﹣x2|最小时,抛物线与直线的交点为D(﹣1,0),E(1,4);
(3)①当P点在AM下方时,如答图1,
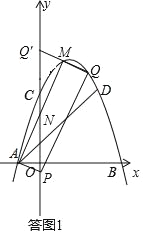
设P(0,p),易知M(1,4),从而Q(2,4+p),
∵△PM Q′与APQM重合部分的面积是APQM面积的![]() ,
,
∴PQ′必过AM中点N(0,2),
∴可知Q′在y轴上,
易知QQ′的中点T的横坐标为1,而点T必在直线AM上,
故T(1,4),从而T、M重合,
∴APQM是矩形,
∵易得直线AM解析式为:y=2x+2,
∵MQ⊥AM,
∴直线QQ′:y=﹣![]() x+
x+![]() ,
,
∴4+p=﹣![]() ×2+
×2+![]() ,
,
解得:p=﹣![]() ,
,
∴PN=![]() ,
,
∴SAPQM=2S△AMP=4S△ANP=4×![]() ×PN×AO=4×
×PN×AO=4×![]() ×
×![]() ×1=5;
×1=5;
②当P点在AM上方时,如答图2,

设P(0,p),易知M(1,4),从而Q(2,4+p),
∵△PM Q′与APQM重合部分的面积是APQM面积的![]() ,
,
∴PQ′必过QM中点R(![]() ,4+
,4+![]() ),
),
易得直线QQ′:y=﹣![]() x+p+5,
x+p+5,
联立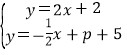 ,
,
解得:x=![]() ,y=
,y=![]() ,
,
∴H(![]() ,
,![]() ),
),
∵H为QQ′中点,
故易得Q′(![]() ,
,![]() ),
),
由P(0,p)、R(![]() ,4+
,4+![]() )易得直线PR解析式为:y=(
)易得直线PR解析式为:y=(![]() ﹣
﹣![]() )x+p,
)x+p,
将Q′(![]() ,
,![]() )代入到y=(
)代入到y=(![]() ﹣
﹣![]() )x+p得:
)x+p得:![]() =(
=(![]() ﹣
﹣![]() )×
)×![]() +p,
+p,
整理得:p2﹣9p+14=0,
解得p1=7,p2=2(与AM中点N重合,舍去),
∴P(0,7),
∴PN=5,
∴SAPQM=2S△AMP=2×![]() ×PN×|xM﹣xA|=2×
×PN×|xM﹣xA|=2×![]() ×5×2=10.
×5×2=10.
综上所述,APQM面积为5或10.

 孟建平名校考卷系列答案
孟建平名校考卷系列答案【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元∕件) | … | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量y与单价x满足一次函数关系,求出y与x的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?