题目内容
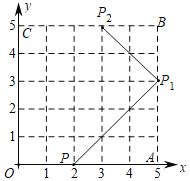
【题目】如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
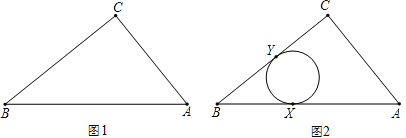
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
【答案】(1)作图见解析;(2)![]() .
.
【解析】
试题(1)作出∠B的角平分线BD,再过X作OX⊥AB,交BD于点O,则O点即为⊙O的圆心;
(2)由于⊙P与△ABC哪两条边相切不能确定,故应分⊙P与Rt△ABC的边AB和BC相切;⊙P与Rt△ABC的边AB和AC相切时;⊙P与Rt△ABC的边BC和AC相切时三种情况进行讨论.
试题解析:(1)如图所示:
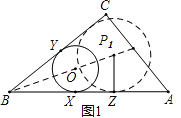
①以B为圆心,以任意长为半径画圆,分别交BC、AB于点G、H;②分别以G、H为圆心,以大于![]() GH为半径画圆,两圆相交于D,连接BD;③过X作OX⊥AB,交直线BD于点O,则点O即为⊙O的圆心.
GH为半径画圆,两圆相交于D,连接BD;③过X作OX⊥AB,交直线BD于点O,则点O即为⊙O的圆心.
(2)①当⊙P与Rt△ABC的边AB和BC相切时,由角平分线的性质可知,动点P是∠ABC的平分线BM上的点,如图1,在∠ABC的平分线BM上任意确定点P1(不为∠ABC的顶点)
∵OX=BOsin∠ABM,P1Z=BPsin∠ABM,当BP1>BO时,P1Z>OX即P与B的距离越大,⊙P的面积越大,这时,BM与AC的交点P是符合题意的、BP长度最大的点; 如图2,
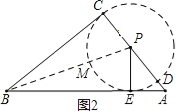
∵∠BPA>90°,过点P作PE⊥AB,垂足为E,则E在边AB上,
∴以P为圆心、PC为半径作圆,则⊙P与CB相切于C,与边AB相切于E,即这时⊙P是符合题意的圆,
时⊙P的面积就是S的最大值,
∵AC=1,BC=2,∴AB=![]() ,
,
设PC=x,则PA=AC-PC=1-x
在直角△APE中,PA2=PE2+AE2,
∴(1-x)2=x2+(![]() -2)2,
-2)2,
∴x=2![]() -4;
-4;
②如图3,
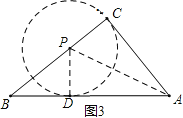
同理可得:当⊙P与Rt△ABC的边AB和AC相切时,设PC=y,则(2-y)2=y2+(![]() -1)2,
-1)2,
∴y=![]() ;
;
③如图4,
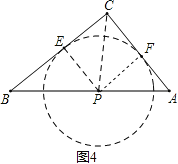
同理可得,当⊙P与Rt△ABC的边BC和AC相切时,设PF=z,
∵△APF∽△PBE,
∴PF:BE=AF:PE,
∴![]() ,
,
∴z=![]() .
.
由①、②、③可知,
![]() >
>![]() >
>![]()
∴z>y>x,
∴⊙P的面积S的最大值为![]() π.
π.
考点:1. 切线的性质;2.角平分线的性质;3.勾股定理;4.作图—复杂作图.