题目内容
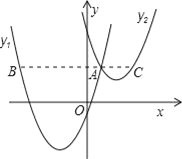
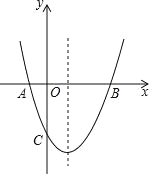
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交于A,B两点(A在B的左侧),顶点为C.
(1)求A,B两点的坐标;
(2)若将该抛物线向上平移t个单位后,它与x轴恰好只有一个交点,求t的值.
【答案】(1)A(﹣1,0),B(3,0);(2)t=4.
【解析】
(1)通过解方程x2-2x-3=0得A点坐标和B点坐标;
(2)利用抛物线的平移规律得到平移后的抛物线解析式为y=x2-2x-3+t,利用判别式的意义得到△=(-2)2-4(-3+t)=0,然后解关于t的方程即可.
解:(1)当y=0时,x2﹣2x﹣3=0,解得x1=3,x2=﹣1,
所以A点坐标为(﹣1,0),B点坐标为(3,0);
(2)抛物线y=x2﹣2x﹣3向上平移t个单位后所得抛物线解析式为y=x2﹣2x﹣3+t,
则△=(﹣2)2﹣4(﹣3+t)=0,
解得t=4.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
相关题目
【题目】手机经销商计划购进苹果手机的 iPhone8、 iphone8Plus、 iphoneX三款手机共60部,每款手机至少要购进10部,且恰好用完购机款360000元.设购进iPhone8手机![]() 部,iPhone8Plus手机
部,iPhone8Plus手机![]() 部.三款手机的进价和售价如表:
部.三款手机的进价和售价如表:
手机型号 | iPhone8 | iphone8Plus | iphoneX |
进价(元部) | 4600 | 6100 | 7600 |
售价(元部) | 5200 | 6800 | 8600 |
(1)用含![]() ,
,![]() 的式子表示购进iphoneX手机的部数.
的式子表示购进iphoneX手机的部数.
(2)求出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)假设所购进手机全部售出.
①求出预估利润![]() (元)与
(元)与![]() (部)的函数关系式.
(部)的函数关系式.
②求出预估利润的最大值,并写出此时购进三款手机各多少部.