题目内容
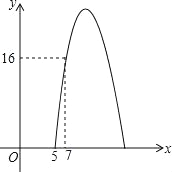
【题目】某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系y=mx2+20x+n,其图象如图所示.
(1)m=_____,n=_____.
(2)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多少元?
(3)该种商品每天的销售利润不低于16元时,直接写出x的取值范围.

【答案】(1)﹣1,﹣75(2)销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元(3)销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元
【解析】
(1)利用待定系数法求二次函数解析式得出即可;
(2)利用配方法求出二次函数最值即可;
(3)根据函数值大于或等于16,可得不等式的解集,可得答案.
(1)y=mx2+20x+n图象过点(5,0)、(7,16),
∴![]() ,
,
解得:![]() ;
;
故答案为:﹣1,﹣75;
(2)∵y=﹣x2+20x﹣75=﹣(x﹣10)2+25,
∴当x=10时,y最大=25.
答:销售单价为10元时,该种商品每天的销售利润最大,最大利润为25元;
(3)∵函数y=﹣x2+20x﹣75图象的对称轴为直线x=10,
可知点(7,16)关于对称轴的对称点是(13,16),
又∵函数y=﹣x2+20x﹣75图象开口向下,
∴当7≤x≤13时,y≥16.
答:销售单价不少于7元且不超过13元时,该种商品每天的销售利润不低于16元.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目