Question

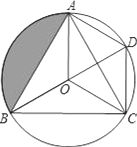
【题目】如图，O是等边△ABC的外心，BO的延长线和⊙O相交于点D，连接DC，DA，OA，OC．

（1）求证：△BOC≌△CDA；

（2）若AB=，求阴影部分的面积．

Answer 1

【答案】（1）证明见解析；（2）S阴影部分=π﹣．

【解析】试题分析：

（1）如图1，由点O是等边△ABC的外心可证得∠1=∠2=30°，由圆周角定理可得：∠5=∠1=30°，∠6=∠2=30°，由OB=OC可得∠3=∠2=30°，结合BC=AC可用“ASA”证得△BOC≌△CDA；

（2）如图2，过点O作OH⊥AB于点H，则由此可得：BH=AB=，∠OHB=90°，设OB= ，则由∠1=30°可得OH= ，在Rt△OHB中由勾股定理建立方程，解方程即可求得；由OB=OA可得∠OAB=∠1=30°，从而可得∠AOB=120°，这样由S阴影 =S扇形AOB-S△AOB即可求出阴影部分的面积了.

试题解析：

（1）证明：如图1所示：

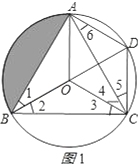
∵O是等边△ABC的外心，

∴BD垂直平分AC

∴∠1=∠2=30°，

∴∠1=∠5=30°，∠2=∠6=30°

∵BO=CO

∴∠2=∠3=30°

∵BC=AC

∴△BOC≌△CDA（SAS）；

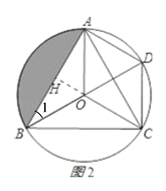
（2）如图2所示，作OH⊥AB于H，

∴BH=AB=，∠OHB=90°，

设OB= ，∵∠1=30°，

∴OH= ，

∴在Rt△OHB中，由勾股定理可得： ，解得： ，则OH=.

∵∠1=30°，OA=OB，

∴∠BAO=∠1=30°，

∴∠AOB=180°-30°-30°=120°，

∴S阴影部分=S扇形AOB﹣S△AOB．