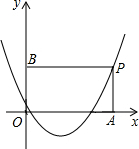
��Ŀ����
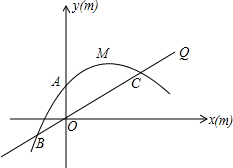
��ͼ���ѡ�OAB������ƽ��ֱ������ϵxOy�У���OAB=90�㣬OA=2��AB=
���ѡ�OAB��x��ĸ�����ƽ��2OA�ij��Ⱥ�õ���DCE��
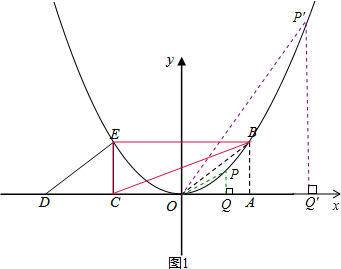
��1������ԭ���������y=ax2+bx+c������B��E����������ߵĽ���ʽ��
��2������P�ڸ����������ƶ�������P�ڵ�һ������ʱ������P��PQ��x���ڵ�Q������OP������O��P��QΪ���������������B��C��EΪ��������������ƣ�ֱ��д����P�����ꣻ
��3������M��-4��n���ڸ��������ϣ�ƽ�������ߣ���ƽ�ƺ��M�Ķ�Ӧ��ΪM�䣬��B�Ķ�Ӧ��ΪB�䣮�����������������ƽ��ʱ���Ƿ����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣������ڣ������ʱ�����ߵĽ���ʽ���������ڣ���˵�����ɣ�
| 3 |
| 2 |
��1������ԭ���������y=ax2+bx+c������B��E����������ߵĽ���ʽ��
��2������P�ڸ����������ƶ�������P�ڵ�һ������ʱ������P��PQ��x���ڵ�Q������OP������O��P��QΪ���������������B��C��EΪ��������������ƣ�ֱ��д����P�����ꣻ
��3������M��-4��n���ڸ��������ϣ�ƽ�������ߣ���ƽ�ƺ��M�Ķ�Ӧ��ΪM�䣬��B�Ķ�Ӧ��ΪB�䣮�����������������ƽ��ʱ���Ƿ����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣������ڣ������ʱ�����ߵĽ���ʽ���������ڣ���˵�����ɣ�

��1��������ã�B(2��
)��
��OC=2��CE=
����E(-2��
)��
�������߾���ԭ��͵�B��E�����������ߵĽ���ʽΪy=ax2��a��0����
�������߾�����B(2��
)��
��
=4a����ã�a=
��
�������ߵĽ���ʽΪy=
x2��
��2���ߵ�P���������ϣ�
�����P��������x��
x2����
�����������
��i������OQP����BECʱ����
=
����
=
����ã�x=1��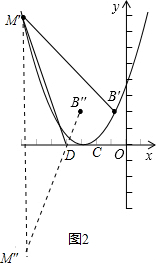
���P��������1��
����
��ii������PQO����BECʱ����
=
����
=
����ã�x=
��
���P��������
��
����
�������������������ĵ�P��������P(1��
)��P(
��
)��
��3�����ڣ�
��Ϊ�߶�M'B'��CD�ij��Ƕ�ֵ������Ҫʹ�ı���M'B'CD���ܳ���̣�ֻҪʹM'D+CB'��̣����������������ƽ�ƣ�
��Ȼ��M��D+CB�䣾MD+CB����˲�����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣���ȻӦ�ý�������y=
x2����ƽ�ƣ�
����֪M��-4��6����
������������ƽ����n����λ�����M'��B�������ֱ�ΪM�䣨-4-n��6����B�䣨2-n��
����
��ΪCD=2����˽���B������ƽ��2����λ��B�壨-n��
����
ҪʹM'D+CB'��̣�ֻҪʹM'D+DB����̣�
��M�����x��ԳƵ������ΪM�壨-4-n��-6����
��ֱ��M��B��Ľ���ʽy=kx+b��k��0������DӦ��ֱ��M��B���ϣ�
��ֱ��M��B��Ľ���ʽΪy=
x+
��B�壨-n��
�����룬���n=
��
�ʽ�����������ƽ��
����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=
(x+
)2��
| 3 |
| 2 |
��OC=2��CE=
| 3 |
| 2 |
| 3 |
| 2 |
�������߾���ԭ��͵�B��E�����������ߵĽ���ʽΪy=ax2��a��0����
�������߾�����B(2��
| 3 |
| 2 |
��
| 3 |
| 2 |
| 3 |
| 8 |
�������ߵĽ���ʽΪy=
| 3 |
| 8 |
��2���ߵ�P���������ϣ�
�����P��������x��
| 3 |
| 8 |
�����������
��i������OQP����BECʱ����
| PQ |
| CE |
| OQ |
| BE |
| ||
|
| x |
| 4 |

���P��������1��
| 3 |
| 8 |
��ii������PQO����BECʱ����
| PQ |
| BE |
| OQ |
| EC |
| ||
| 4 |
| x | ||
|
| 64 |
| 9 |
���P��������
| 64 |
| 9 |
| 512 |
| 27 |
�������������������ĵ�P��������P(1��
| 3 |
| 8 |
| 64 |
| 9 |
| 512 |
| 27 |
��3�����ڣ�
��Ϊ�߶�M'B'��CD�ij��Ƕ�ֵ������Ҫʹ�ı���M'B'CD���ܳ���̣�ֻҪʹM'D+CB'��̣����������������ƽ�ƣ�
��Ȼ��M��D+CB�䣾MD+CB����˲�����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣���ȻӦ�ý�������y=
| 3 |
| 8 |
����֪M��-4��6����
������������ƽ����n����λ�����M'��B�������ֱ�ΪM�䣨-4-n��6����B�䣨2-n��
| 3 |
| 2 |
��ΪCD=2����˽���B������ƽ��2����λ��B�壨-n��
| 3 |
| 2 |
ҪʹM'D+CB'��̣�ֻҪʹM'D+DB����̣�
��M�����x��ԳƵ������ΪM�壨-4-n��-6����
��ֱ��M��B��Ľ���ʽy=kx+b��k��0������DӦ��ֱ��M��B���ϣ�
��ֱ��M��B��Ľ���ʽΪy=
| 6 |
| n |
| 24 |
| n |
��B�壨-n��
| 3 |
| 2 |
| 16 |
| 5 |
�ʽ�����������ƽ��
| 16 |
| 5 |
| 3 |
| 8 |
| 16 |
| 5 |


��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 Ϊԭ�㣬OA����ֱ��Ϊy�ᣬ��O�㴹ֱ��OA��ֱ��Ϊx�Ὠ��ֱ������ϵ����ˮ�絽б���ϵ���͵�ΪB����ߵ�ΪC��
Ϊԭ�㣬OA����ֱ��Ϊy�ᣬ��O�㴹ֱ��OA��ֱ��Ϊx�Ὠ��ֱ������ϵ����ˮ�絽б���ϵ���͵�ΪB����ߵ�ΪC��

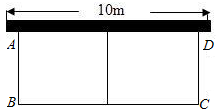 ��ʣ�һ�濿ǽ��ǽ��Ϊ10m�����軨�Կ�ABΪx��m�������ΪS��m2����
��ʣ�һ�濿ǽ��ǽ��Ϊ10m�����軨�Կ�ABΪx��m�������ΪS��m2����