题目内容
已知平面直角坐标系xOy中,点A在抛物线y=
x2+
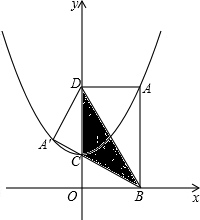
上,过A作AB⊥x轴于点B,AD⊥y轴于点D,将矩形ABOD沿对角线BD折叠后得A的对应点为A′,重叠部分(阴影)为△BDC.
(1)求证:△BDC是等腰三角形;
(2)如果A点的坐标是(1,m),求△BDC的面积;
(3)在(2)的条件下,求直线BC的解析式,并判断点A′是否落在已知的抛物线上?请说明理由.
2
| ||
| 3 |
| ||
| 3 |
(1)求证:△BDC是等腰三角形;
(2)如果A点的坐标是(1,m),求△BDC的面积;
(3)在(2)的条件下,求直线BC的解析式,并判断点A′是否落在已知的抛物线上?请说明理由.

(1)证明:由折叠的性质之:∠ABD=∠DBC,
∵四边形ABOD是矩形
∴AB∥DO
∴∠ABD=∠CDB
∴∠CBD=∠BDC
∴△BDC是等腰三角形.
(2)∵点A(1,m)在y=
x2+
上,
∴m=
+
=
.
在直角三角形ABD中,AB=
,DA=1,
∴∠ABD=30°,
∴∠CBO=30°,CO=OB•tan∠CBO=
,
S△BCD=S△BDO-S△BCO=
OD•OB-
OB•OC=
-
×
=
.
(3)设直线BC解析式为:y=ax+b,
∵C(0,
),B(1,0);
∴
,
解得
,
y=-
+
,
设A′的坐标为(x,y),过A′作A′M⊥x轴于M,
A′M=
BA′=
AB=
,
∴y=
,
代入y=-
+
,
得x=-
,
点A′的坐标是(-
,
),
将x=-
代入y=
x2+
中
得:y=
,
∴A′落在此抛物线上.
∵四边形ABOD是矩形
∴AB∥DO
∴∠ABD=∠CDB
∴∠CBD=∠BDC
∴△BDC是等腰三角形.
(2)∵点A(1,m)在y=
2
| ||
| 3 |
| ||
| 3 |
∴m=
2
| ||
| 3 |
| ||
| 3 |
| 3 |
在直角三角形ABD中,AB=
| 3 |
∴∠ABD=30°,
∴∠CBO=30°,CO=OB•tan∠CBO=
| ||
| 3 |
S△BCD=S△BDO-S△BCO=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 3 |
| ||
| 3 |
(3)设直线BC解析式为:y=ax+b,
∵C(0,
| ||
| 3 |
∴
|

解得
|
y=-
| ||
| 3 |
| ||
| 3 |
设A′的坐标为(x,y),过A′作A′M⊥x轴于M,
A′M=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴y=
| ||
| 2 |
代入y=-
| ||
| 3 |
| ||
| 3 |
得x=-
| 1 |
| 2 |
点A′的坐标是(-
| 1 |
| 2 |
| ||
| 2 |
将x=-
| 1 |
| 2 |
2
| ||
| 3 |
| ||
| 3 |
得:y=
| ||
| 2 |
∴A′落在此抛物线上.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
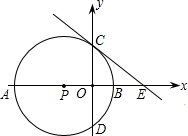 D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.
D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.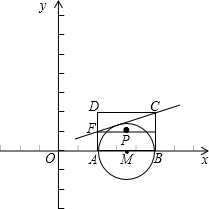 半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线
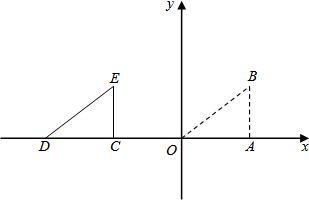
半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线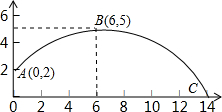 某个二次函数图象的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5).
某个二次函数图象的一部分,如图所示,如果这个男同学的出手处A点的坐标(0,2),铅球路线的最高处B点的坐标为(6,5).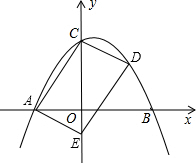
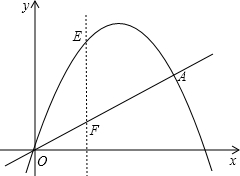 x的图象交于O、A两点.
x的图象交于O、A两点.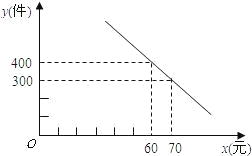 间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?