题目内容
已知:a、b、c分别是△ABC的∠A、∠B、∠C的对边(a>b).二次函数y=(x-2a)x-2b(x-a)+c2的图象的顶点在x轴上,且sinA、sinB是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两个根.
(1)判断△ABC的形状,关说明理由;
(2)求m的值;
(3)若这个三角形的外接圆面积为25π,求△ABC的内接正方形(四个顶点都在三角形三边上)的边长.
(1)判断△ABC的形状,关说明理由;
(2)求m的值;
(3)若这个三角形的外接圆面积为25π,求△ABC的内接正方形(四个顶点都在三角形三边上)的边长.
(1)△ABC是直角三角形,理由如下:
将y=(x-2a)x-2b(x-a)+c2化简,整理得:y=x2-2(a+b)x+2ab+c2,
∵此函数图象的顶点在x轴上,
∴
=0,
整理,得a2+b2=c2,
∴△ABC是直角三角形;
(2)∵△ABC是直角三角形,∠C=90°,
∴∠A+∠B=90°,
∴sinB=cosA,
∴sinA、cosA是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两个根,
∴
,
又∵sin2A+cos2A=1,
∴(sinA+cosA)2-2sinA•cosA=1,
∴(
)2-2×
=1,
整理,得m2-24m+80=0,
解得m1=20,m2=4.
经检验,m1=20,m2=4都是原方程的根,
但是,当m1=20时,sinA+cosA>0,sinA•cosA>0,
当m2=4时,sinA+cosA>0,sinA•cosA<0,舍去,
∴m=20;
 (3)∵△ABC的外接圆面积为25π,
(3)∵△ABC的外接圆面积为25π,
∴外接圆半径R=5,
∴斜边c=10.
当m=20时,原方程变为25x2-35x+12=0,
解得x1=
,x2=
,
∴a=8,b=6.
设正方形的边长为x.
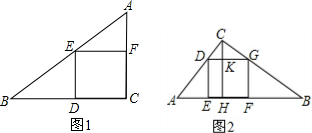
图1中,由EF:BC=AF:AC,得x:8=(6-x):6,
解得x=
;
图2中,CH=
,
CK:CH=DG:AB,(
-x):
=x:10,
解得x=
.
综上可知,△ABC的内接正方形(四个顶点都在三角形三边上)的边长为
或
.
将y=(x-2a)x-2b(x-a)+c2化简,整理得:y=x2-2(a+b)x+2ab+c2,
∵此函数图象的顶点在x轴上,
∴
| 4(2ab+c2)-4(a+b)2 |
| 4 |
整理,得a2+b2=c2,
∴△ABC是直角三角形;
(2)∵△ABC是直角三角形,∠C=90°,
∴∠A+∠B=90°,
∴sinB=cosA,
∴sinA、cosA是关于x的方程(m+5)x2-(2m-5)x+m-8=0的两个根,
∴
|
又∵sin2A+cos2A=1,
∴(sinA+cosA)2-2sinA•cosA=1,
∴(
| 2m-5 |
| m+5 |
| m-8 |
| m+5 |
整理,得m2-24m+80=0,
解得m1=20,m2=4.
经检验,m1=20,m2=4都是原方程的根,
但是,当m1=20时,sinA+cosA>0,sinA•cosA>0,
当m2=4时,sinA+cosA>0,sinA•cosA<0,舍去,
∴m=20;
 (3)∵△ABC的外接圆面积为25π,
(3)∵△ABC的外接圆面积为25π,∴外接圆半径R=5,
∴斜边c=10.
当m=20时,原方程变为25x2-35x+12=0,
解得x1=
| 4 |
| 5 |
| 3 |
| 5 |
∴a=8,b=6.
设正方形的边长为x.
图1中,由EF:BC=AF:AC,得x:8=(6-x):6,
解得x=
| 24 |
| 7 |
图2中,CH=
| 24 |
| 5 |
CK:CH=DG:AB,(
| 24 |
| 5 |
| 24 |
| 5 |
解得x=
| 120 |
| 37 |
综上可知,△ABC的内接正方形(四个顶点都在三角形三边上)的边长为
| 24 |
| 7 |
| 120 |
| 37 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?