题目内容
如图,P为抛物线y=
x2-
x+
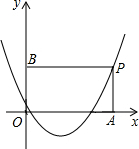
上对称轴右侧的一点,且点P在x轴上方,过点P作PA垂直x轴于点A,PB垂直y轴于点B,得到矩形PAOB.若AP=1,求矩形PAOB的面积.
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |

∵PA⊥x轴,AP=1,
∴点P的纵坐标为1.
当y=1时,
x2-
x+
=1,
即x2-2x-1=0.
解得x1=1+
,x2=1-
.
∵抛物线的对称轴为直线x=1,点P在对称轴的右侧,
∴x=1+
.
∴矩形PAOB的面积为(1+
)个平方单位.
∴点P的纵坐标为1.
当y=1时,
| 3 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
即x2-2x-1=0.
解得x1=1+
| 2 |
| 2 |
∵抛物线的对称轴为直线x=1,点P在对称轴的右侧,
∴x=1+
| 2 |
∴矩形PAOB的面积为(1+
| 2 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

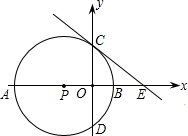 D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.
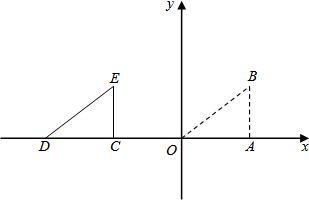
D,其中A(-3,0),B(1,0).过点C作⊙P的切线交x轴于点E.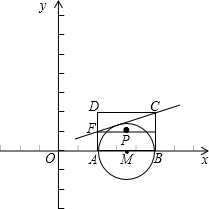 半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线
半轴上,点A在点B的左侧,另两个顶点都在第一象限,且直线
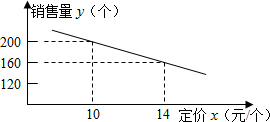 个星期的销售量y(个)与它的定价x(元/个)的关系如图所示:
个星期的销售量y(个)与它的定价x(元/个)的关系如图所示: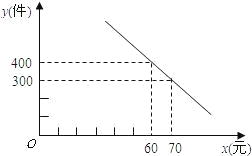 间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?
间的函数关系式,并写出自变量x的取值范围;根据题意判断:当x取何值时,P的值最大,最大值是多少?