题目内容
【题目】如图,平面直角坐标系中,直线y=![]() x+4
x+4![]() 分别交x轴、y轴于点A、C,直线BC与直线AC关于y轴对称,动点D从点A出发,沿AC以每秒2个单位长度的速度向终点C运动,当点D出发后,过点D作DE∥BC交折线A﹣O﹣C于点E,以DE为边作等边△DEF,设△DEF与△ACO重叠部分图形的面积为S,点D运动的时间为t秒.
分别交x轴、y轴于点A、C,直线BC与直线AC关于y轴对称,动点D从点A出发,沿AC以每秒2个单位长度的速度向终点C运动,当点D出发后,过点D作DE∥BC交折线A﹣O﹣C于点E,以DE为边作等边△DEF,设△DEF与△ACO重叠部分图形的面积为S,点D运动的时间为t秒.
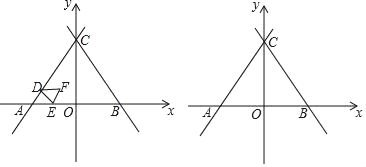
(1)写出坐标:点A( ),点B( ),点C( );
(2)当点E在线段AO上时,求S与t之间的函数关系式;
(3)求出以点B、E、F为顶点的三角形是直角三角形时t的值;
(4)直接写出点F运动的路程长为 .
【答案】(1)﹣4,0;4,0;0,4![]() ;(2)S=﹣
;(2)S=﹣![]() ;(3)t的值是
;(3)t的值是![]() 秒或
秒或![]() 秒;(4)4
秒;(4)4![]() +4.
+4.
【解析】
(1)令x=0,得![]() 即可求出点
即可求出点![]() 的坐标,令y=0,得
的坐标,令y=0,得![]() 即可求出点
即可求出点![]() 的坐标,根据直线BC与直线AC关于y轴对称,即可求出点
的坐标,根据直线BC与直线AC关于y轴对称,即可求出点![]() 的坐标.
的坐标.
(2)当点F在OC上时,求出![]() 的值,然后分两种情况进行讨论即可.
的值,然后分两种情况进行讨论即可.
(3)分∠EFB=90°和∠FEB=90°两种情况进行讨论,分别画出示意图,进行计算即可.
(4)点E在线段OA上时,如图,点F的运动路径为等边△ACB中BC边上的高线AF,
当点E在线段OC上时,设BC的中点为P,如图点F的运动路径为PC的长,相加即可.
(1)x=0时,![]()
∴![]()
当y=0时,![]()
∴![]()
∵直线BC与直线AC关于y轴对称,
∴B(4,0),
故答案为:﹣4,0;4,0;0,![]()
(2)Rt△ACO中, ![]()
∴∠CAO=60°,
∵AC=BC,
∴∠ABC=∠CAO=60°,
∵DE∥BC,
∴∠AED=∠ABC=60°,
∴△ADE是等边三角形,
∴AD=AE=2t,
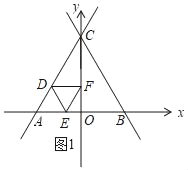
当点F在OC上时,如图1,
∵∠AED=∠DEF=60°,
∴∠OEF=30°,
∵∠EOF=90°,
∵EF=DE=AD=2t,
∴![]()
∵AO=AE+OE=2t+t=4,
![]()
①当![]() 时,点E在线段OA上,△DEF与△ACO重叠部分图形是△DEF,如图2,
时,点E在线段OA上,△DEF与△ACO重叠部分图形是△DEF,如图2,
![]()
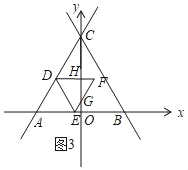
②当![]() 时,如图3,△DEF与△ACO重叠部分图形是四边形DEGH,
时,如图3,△DEF与△ACO重叠部分图形是四边形DEGH,
∵AE=2t,OE=4﹣2t,
Rt△EOG中,∠EGO=30°,
∴![]()
![]()
Rt△FHG中,∠HGF=30°,
∴![]()
∴S=S△DEF﹣S△GHF,
![]()
![]()
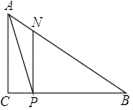
(3)①如图4,当0<t≤2时,∠EFB=90°,∠FBE=30°,
∴BE=2EF=2AD,
则8﹣2t=4t,
![]()
②如图5,当2<t<4时,E在y轴上,
∠FEB=90°,∠FBE=30°,
∵∠ABC=60°,
∴∠EBO=30°,
∵OB=4,
∴![]()
∴![]()
∵BF=AD,
∴![]()
![]()
综上,t的值是![]() 秒或
秒或![]() 秒;
秒;
(4)动点D从点A出发,DE∥BC,点E在线段OA上时,如图6,点F的运动路径为等边△ACB中BC边上的高线AF,
此时![]()
当点E在线段OC上时,设BC的中点为P,如图7,点F的运动路径为PC的长,
∵![]()
∴点F运动的路程长为:![]()
故答案为:![]()