ЬтФПФкШн
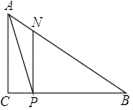
ЁОЬтФПЁПШчЭМдкЁїABCжаЃЌЁЯC=90ЁуЃЌAC=3cmЃЌBC=4cmЃЌЕуPЪЧБпBCЩЯгЩBЯђCдЫЖЏЃЈВЛгыЕуBЁЂCжиКЯЃЉЕФвЛЖЏЕуЃЌPЕуЕФЫйЖШЪЧ1cm/sЃЌЩшЕуPЕФдЫЖЏЪБМфЮЊtЃЌЙ§PЕузїACЕФЦНааЯпНЛABгыЕуNЃЌСЌНгAPЃЌ
ЃЈ1ЃЉЧыгУКЌгаtЕФДњЪ§ЪНБэЪОЯпЖЮANКЭЯпЖЮPNЕФГЄЃЌ
ЃЈ2ЃЉЕБtЮЊКЮжЕЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃП
ЃЈ3ЃЉдкЕуPЕФдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкФГвЛЪБПЬЕФtЕФжЕЃЌЪЙЕУЁїAPNЕФУцЛ§газюДѓжЕЃЌШєДцдкЧыЧѓГіtЕФжЕВЂМЦЫузюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ PN=![]() tЃЌAN =5Љ
tЃЌAN =5Љ![]() tЃЛЃЈ2ЃЉЕБtЮЊ
tЃЛЃЈ2ЃЉЕБtЮЊ![]() sЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃЛЃЈ3ЃЉt=2ЪБЃЌЁїPANЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ
sЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃЛЃЈ3ЃЉt=2ЪБЃЌЁїPANЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУЙДЙЩЖЈРэЧѓГіABЃЌдйРћгУЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЃЌЧѓГіPNЁЂBNМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉгЩЬтвтЃК![]() PNPCЃН
PNPCЃН![]() ЁС
ЁС![]() PCACЃЌЭЦГіACЃН3PNЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
PCACЃЌЭЦГіACЃН3PNЃЌгЩДЫЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЛ
ЃЈ3ЃЉЙЙНЈЖўДЮКЏЪ§ЃЌРћгУЖўДЮКЏЪ§ЕФаджЪМДПЩНтОіЮЪЬт.
ЃЈ1ЃЉдкRtЁїABCжаЃЌЁпЁЯC=90ЁуЃЌAC=3cmЃЌBC=4cmЃЌ
ЁрAB=![]() =5ЃЈcmЃЉЃЌ
=5ЃЈcmЃЉЃЌ
ЁпPNЁЮACЃЌPB=tЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
ЁрBN=![]() tЃЌPN=
tЃЌPN=![]() tЃЌ
tЃЌ
ЁрAN=ABЉBN=5Љ![]() tЃЎ
tЃЎ
ЃЈ2ЃЉгЩЬтвтЃК![]() PNPC=
PNPC=![]() ЁС
ЁС![]() PCACЃЌ
PCACЃЌ
ЁрAC=3PNЃЌ
Ёр3=3![]() tЃЌ
tЃЌ
Ёрt=![]() ЃЌ
ЃЌ
ЁрЕБtЮЊ2sЪБЃЌЁїAPNЕФУцЛ§ЕШгкЁїACPУцЛ§ЕФШ§ЗжжЎвЛЃЎ
ЃЈ3ЃЉгЩЬтвтЃКSЁїAPN=![]() PNPC=
PNPC=![]()
![]() tЃЈ4ЉtЃЉ=Љ
tЃЈ4ЉtЃЉ=Љ![]() ЃЈtЉ2ЃЉ2+
ЃЈtЉ2ЃЉ2+![]() ЃЌ
ЃЌ
ЁпЉ![]() ЃМ0ЃЌ
ЃМ0ЃЌ
Ёрt=2ЪБЃЌЁїPANЕФУцЛ§зюДѓЃЌзюДѓжЕЮЊ![]() ЃЎ
ЃЎ