Question

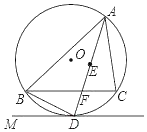
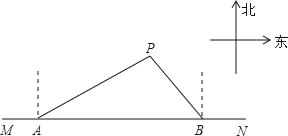
【题目】如图，BC为Rt△ABC的斜边，∠CBA＝30°，△ABD，△ACF，△BCE均为正三角形，四边形MNPE是长方形，点F在MN上，点D在NP上，若AC＝2，则图中空白部分的面积是_____．

Answer 1

【答案】13．

【解析】

由等边三角形的性质得出BE＝CE＝BC，∠BCE＝∠BEC＝∠CBE＝∠ABD＝∠ACF＝60°，CF＝AC＝2，BD＝AB，由直角三角形的性质得出CE＝BE＝BC＝2AC＝4，BD＝AB＝AC＝2，证明E、C、F三点共线，得出EF＝CE+CF＝6，由直角三角形的性质得出MF＝EF＝3，EM＝MF＝3，PD＝BD＝，BP＝PD＝3，得出PE＝BE+BP＝7，则图中空白部分的面积＝矩形MNPE的面积﹣△BCE的面积﹣△ABD的面积﹣△ACF的面积，即可得出答案．

∵△ABD，△ACF，△BCE均为正三角形，

∴BE＝CE＝BC，∠BCE＝∠BEC＝∠CBE＝∠ABD＝∠ACF＝60°，CF＝AC＝2，BD＝AB，

∵BC为Rt△ABC的斜边，∠CBA＝30°，

∴∠ACB＝60°，CE＝BE＝BC＝2AC＝4，BD＝AB＝AC＝2，

∵∠BCE+∠ACB+∠ACF＝180°，

∴E、C、F三点共线，

∴EF＝CE+CF＝6，

∵四边形MNPE是长方形，

∴∠M＝∠MEP＝∠P＝90°，

∴∠MEF＝90°﹣60°＝30°，

∴MF＝EF＝3，EM＝MF＝3，

∵∠DBE＝60°+30°+60°＝150°，

∴∠PBD＝30°，

∴PD＝BD＝，BP＝PD＝3，

∴PE＝BE+BP＝7，

∴图中空白部分的面积＝矩形MNPE的面积﹣△BCE的面积﹣△ABD的面积﹣△ACF的面积＝；

故答案是：13．