��Ŀ����
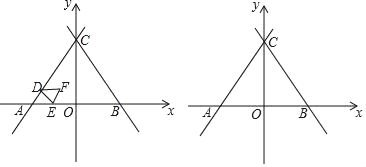
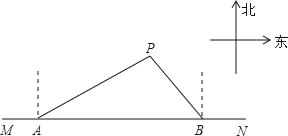
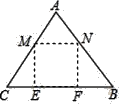
����Ŀ����ͼ����үү��Ժ������һ�����������ABC��AB=AC=5�ף�BC=6�ף��ִ���������ѳ�һ������MNFE������ֲ�²ˣ���AMN������ֲ�۲ˣ���CME����BNF������ֲ��ˣ��������������ľ����Բ��ƣ������е�M��N�ֱ���AC��AB�ϣ���E��F��BC�ϣ���֪�²�ÿƽ��������100Ԫ���۲�ÿƽ��������60Ԫ�����ÿƽ��������40Ԫ����CM=5x�ף���үү���߲�������ΪWԪ��
��1��������MNFEǡ��Ϊ������ʱ����²���ֲ�������MNFE�������
��2������ֲ�²˵���������������߲�����֮�͵�2��������ʱx��ֵ��
��3������үү���߲�������ΪW����x�ĺ�������ʽ��W�����ֵ��
���𰸡���1��![]() ����2��x=
����2��x=![]() ��
��![]() ;(3)W=��1200��x��
;(3)W=��1200��x��![]() ��2+912��x=
��2+912��x=![]() ʱ��W�����ֵ�����ֵΪ912Ԫ
ʱ��W�����ֵ�����ֵΪ912Ԫ
��������
��1�����ݳɱ�������һ��δ֪����ͨ�����ɶ������.��2���ô���ʽ��ʾ�����߲˵����棬���������γɵ�ʽ���Ӷ���⣬�ó�x.��3����x��ʾ�������߲˵����棬���ΪW���Ӷ���������ʽ���ö��κ�������������ֵ.
��1����AH��BC��H����MN��D��
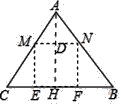
��AB=AC��AH��BC��
��CH=HB=3��
��Rt��ACH��AH=![]() =4��
=4��
��ME��AH��
��![]() =
=![]() =
=![]() ��
��
��CE=3x��EM=EF=4x��
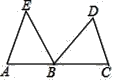
��֤��MEC�ա�NFB��
��CE=BF=3x��
��3x+4x+3x=6��
��x=![]() ��
��
��EM=![]() ��
��
�����MNFE�����Ϊ![]() ƽ���ף�
ƽ���ף�
��2�������⣺100��4x��6��6x��=2[60��![]() ����6��6x����4��4x��+40��4x��3x]��
����6��6x����4��4x��+40��4x��3x]��
���x=![]() ��
��![]() ��
��
��3��������W=100��4x��6��6x��+60��![]() ����6��6x����4��4x��+40��4x��3x=��1200x2+960x+720=��1200��x��
����6��6x����4��4x��+40��4x��3x=��1200x2+960x+720=��1200��x��![]() ��2+912��
��2+912��
������1200��0��
��x=![]() ʱ��W�����ֵ�����ֵΪ912Ԫ��
ʱ��W�����ֵ�����ֵΪ912Ԫ��

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д�����Ŀ��ijУ����������ѡ����ѡһ���μ�ȫ����Сѧ�˶��������![]() ������Ŀ����УԤ�ȶ�������ѡ�ֲ�����
������Ŀ����УԤ�ȶ�������ѡ�ֲ�����![]() �Σ����Գɼ����±�
�Σ����Գɼ����±�
|
|
|
|
|
|
|
| |
�ijɼ����룩 |
|
|
|
|
|
|
|
|
�ҵijɼ����룩 |
|
|
|
|
|
|
|
|
![]() Ϊ�˺���������ѡ��
Ϊ�˺���������ѡ��![]() ���ܵ�ˮƽ����ѡ����Щͳ��������ֱ������Щͳ������ֵ��
���ܵ�ˮƽ����ѡ����Щͳ��������ֱ������Щͳ������ֵ��
![]() ����Ϊѡ��˭�ȽϺ��ʣ�Ϊʲô��
����Ϊѡ��˭�ȽϺ��ʣ�Ϊʲô��