ЬтФПФкШн
ЁОЬтФПЁПФГаЃдкЭЦНјаТПЮИФЕФЙ§ГЬжаЃЌПЊЩшЕФЁАПЮГЬГЌЪаЁБгаЃКAЃЎьХВЪОчЩчЃЌBЃЎХытПЃЌCЃЎгЮгОЃЌDЃЎг№УЋЧђЃЌEЃЎПЦММЕШЮхИіПЦФПЃЌбЇЩњПЩИљОнздМКЕФАЎКУбЁаовЛУХЃЌИКд№ЁАПЮГЬГЌЪаЁБЕФРЯЪІЖдЦпФъМЖвЛАрШЋЬхЭЌбЇЕФбЁПЮЧщПіНјааЕїВщЭГМЦЃЌВЂНЋНсЙћЛцжЦГЩСЫШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃК
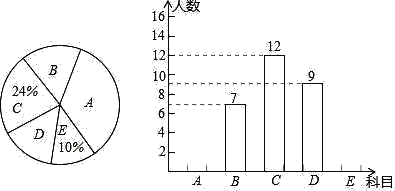
ИљОнЭМжаЬсЙЉЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыЧѓГіИУАрЕФзмШЫЪ§ЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЃЌDЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊЁЁ ЁЁЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉИУАрАрЮЏ4ШЫжаЃЌ1ШЫбЁаоьХВЪОчЩчЃЌ2ШЫбЁаоХытПЃЌ1ШЫбЁаогЮгОЃЌРЯЪІвЊДгет4ШЫжаШЮбЁ2ШЫСЫНтЫћУЧЖдЁАПЮГЬГЌЪаЁБПЮГЬАВХХЕФПДЗЈЃЌЧыФугУСаБэЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓбЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЕФИХТЪЃЎ
ЁОД№АИЁПЃЈ1ЃЉ50ЃЛЃЈ2ЃЉ64.8ЁуЃЌЭМЯъМћНтЮіЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
(1)гУCзщЕФШЫЪ§Г§вдЫќЫљеМЕФАйЗжБШМДПЩЕУЕНШЋАрШЫЪ§;
(2)гУDзщЕФЫљеМАйЗжБШГЫвд360ЁЃМДПЩЕУЕНдкЩШаЮЭГМЦЭМжа"DЁБЖдгІЩШаЮЕФдВаФНЧЕФЖШЪ§ЃЌЯШМЦЫуГіEзщШЫЪ§КЭAзщШЫЪ§ЃЌШЛКѓВЙШЋЦЕЪ§ЗжВМжБЗНЭМ;
(3)ЯШЛЪїзДЭМеЙЪОЫљга12жжЕШПЩФмЕФНсЙћЪ§ЃЌевГібЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЫљеМНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНт.
ЃЈ1ЃЉИУАрЕФзмШЫЪ§ЮЊ12ЁТ24%=50ЃЈШЫЃЉЃЌ
ЙЪД№АИЮЊЃК50ЃЛ
ЃЈ2ЃЉБэЪОDЫљдкЩШаЮЕФдВаФНЧЪЧ360ЁуЁС![]() =64.8ЁуЃЌ
=64.8ЁуЃЌ
EПЦФПШЫЪ§ЮЊ50ЁС10%=5ЃЈШЫЃЉЃЌAПЦФПШЫЪ§ЮЊ50ЉЃЈ7+12+9+5ЃЉ=17ЃЈШЫЃЉЃЌ
ВЙШЋЭМаЮШчЯТЃК
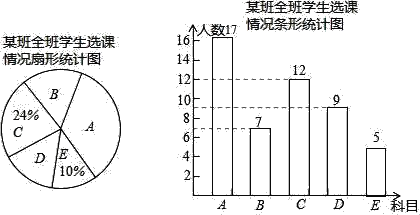
ЙЪД№АИЮЊЃК64.8ЁуЃЛ
ЃЈ3ЃЉЛЪїзДЭМЮЊЃК
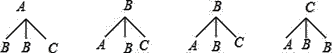
ЙВга12жжЕШПЩФмЕФНсЙћЪ§ЃЌЦфжабЁГіЕФ2ШЫжаЃЌ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЕФеМ4жжЃЌЫљвдбЁГіЕФ2ШЫЧЁКУ1ШЫбЁаоьХВЪОчЩчЃЌ1ШЫбЁаоХытПЕФИХТЪ=![]() =
=![]() ЃЎ
ЃЎ