Question

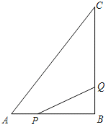
【题目】如图，等腰△ABC中，AB=AC=10，BC=16，点F是边BC上不与点B，C重合的一个动点，直线DE垂直平分BF，垂足为D.当△ACF是直角三角形时，线段BD的长为__________.

Answer 1

【答案】4或．

【解析】

分两种情况讨论：

①当∠AFC=90°时，AF⊥BC，利用等腰三角形的三线合一性质和垂直平分线的性质可解；
②当∠CAF=90°时，过点A作AM⊥BC于点M，证明△AMC∽△FAC，列比例式求出FC，从而得BF，再利用垂直平分线的性质得BD．

①当∠AFC=90°时，AF⊥BC，
∵AB=AC，
∴BF=BC=8
∵DE垂直平分BF，
∴BD=BF=4；

②当∠CAF=90°时，过点A作AM⊥BC于点M，
∵AB=AC，
∴BM=CM，
在Rt△AMC与Rt△FAC中，∠AMC=∠FAC=90°，∠C=∠C，
∴△AMC∽△FAC，
∴，
∴FC=，
∵AC=10，MC=BC=8，
∴FC=，

∴BF=BC-FC=16-=，
∴BD=BF=.

故答案为：4或．