��Ŀ����
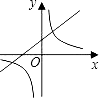
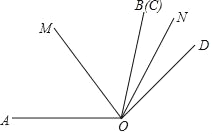
����Ŀ����ͼ����AOB��������COD����������������OC��OB�غϣ�OD�ڡ�AOB�⣬����OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
��1����������100��������60�������MON���ڶ��٣�
���ڢٵ������¡�COD�Ƶ�O��ʱ����תn����0��n��100����n��60��ʱ�����MON�Ķ�����
��2��ֱ��д����COD�Ƶ�O��ʱ����תn����0��n��360��ʱ��MON��ֵ���ú���������ʽ�ӱ�ʾ����
���𰸡���1���١�MON��80�㣻�ڡ�MON��80�㣻��2����MON��![]() ����+������180�㩁
����+������180�㩁![]() ����+������
����+������
��������
��1���ٸ��ݽ�ƽ���ߵĶ��������BOM�͡�CON�Ķ�����Ȼ����Ӽ��ɵó��𰸣�
�ڸ�����ת�����ʿ�֪��BOC=n�㣬����������������ۣ���ͼ1����BOD��60�㩁n�㣬��AOC��100����n�������ݽ�ƽ���ߵĶ���ó���COM�͡�BON�Ķ�����Ȼ����ݡ�MON����COM+��COB+��BON���м��㼴�ɵó����ۣ���ͼ2����BOD��n����60������AOC��100����n�������ݽ�ƽ���ߵĶ���ó���COM�͡�BON�Ķ�����Ȼ����ݡ�MON����COM+��COD+��BON���м��㼴�ɵó����ۣ�
��2�����ݢ١��ڵĽ���˼·���ɵõ����ۣ�
��1���١�OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
���BOM��![]() ��AOB����BON��
��AOB����BON��![]() ��BOD��
��BOD��
���MON��![]() ����AOB+��BOD����
����AOB+��BOD����
�֡ߡ�AOB��100������COD��60����
���MON��![]() ����AOB+��BOD����
����AOB+��BOD����![]() ����100��+60������80����
����100��+60������80����
����ͼ1���ߡ�COD�Ƶ�O��ʱ����תn����
���BOC��n����
���BOD��60����n������AOC��100����n����
��OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
���COM��![]() ��AOC��50����
��AOC��50����![]() n������BON��
n������BON��![]() ��BOD��30����
��BOD��30����![]() n����
n����
���MON����COM+��COB+��BON��80����
��ͼ2���ߡ�COD�Ƶ�O��ʱ����תn����
���BOC��n����
���BOD��n����60������AOC��100����n����
��OM��ON�ֱ��ǡ�AOC����BOD�Ľ�ƽ���ߣ�
���COM��![]() ��AOC��50����
��AOC��50����![]() n������DON��
n������DON��![]() ��BOD��
��BOD��![]() n����30����
n����30����
���MON����COM+��COD+��DON��80����
��2����OMΪ��AOD��ƽ���ߣ�ONΪ��BOC��ƽ���ߣ���AOB��������COD������
���MON��![]() ����+������180����
����+������180����![]() ����+������
����+������