题目内容
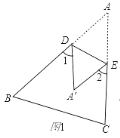
【题目】如图,AB是⊙O的直径,点C在⊙O上,∠CAB的平分线交⊙O于点D,过点D作AC的垂线交AC的延长线于点E,连接BC交AD于点F.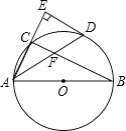
(1)猜想ED与⊙O的位置关系,并证明你的猜想;
(2)若AB=6,AD=5,求AF的长.
【答案】
(1)解:ED与⊙O的位置关系是相切.理由如下:
连接OD,
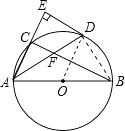
∵∠CAB的平分线交⊙O于点D,
∴ ![]() =
= ![]() ,
,
∴OD⊥BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∵DE⊥AC,
∴DE∥BC,
∴OD⊥DE,
∴ED与⊙O的位置关系是相切。
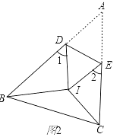
(2)解:连接BD.
∵AB是直径,
∴∠ADB=90°,
在Rt△ABD中,BD= ![]() =
= ![]() =
= ![]() ,
,
∵AB为直径,
∴∠ACB=∠ADB=90°,
又∵∠AFC=∠BFD,
∴∠FBD=∠CAD=∠BAD
∴△FBD∽△BAD,
∴ ![]() =
= ![]()
∴FD= ![]()
∴AF=AD﹣FD=5﹣ ![]() =
= ![]() .
.
【解析】(1)要证ED与⊙O相切,可知点D在⊙O,由此连接OD,根据∠CAB的平分线交⊙O于点D,证得弧CD=弧BD,再根据垂径定理得出OD⊥BC,根据直径所对的圆周角是直角,证得BC⊥AC,然后证明DE∥BC,由DE⊥AC,即可证得结论。
(2)先在Rt△ABD中,利用勾股定理求出BD的长,再证明△FBD∽△BAD,得出对应边成比例。求出FD的长,根据AF=AD﹣FD,即可得出AF的长
【考点精析】本题主要考查了垂径定理和圆周角定理的相关知识点,需要掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目