Question

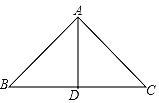
【题目】已知：如图，A、B、C为⊙O上的三个点，⊙O的直径为4cm，∠ACB=45°，求AB的长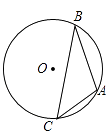

Answer 1

【答案】解：连接OA，OB，

∵∠ACB=45°，

∴∠AOB=2∠ACB=90°，

∵⊙O的直径为4cm，

∴OA=OB=2cm，

∴AB= （cm）

【解析】抓住题中根据的已知条件，圆周角∠ACB=45°，根据圆周角定理即可添加辅助线构造圆心角是直角，因此连接OA、OB，先求出半径的长，再利用勾股定理求出AB的长。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2，以及对圆周角定理的理解，了解顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．