题目内容
【题目】如图，正方形ABCD中，AB=4cm，点E、F同时从C点出发，以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动，到点A时停止运动．设运动时间为t（s），△AEF的面积为S（cm2），则S（cm2）与t（s）的函数关系可用图象表示为（ ）
A.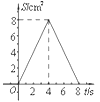
B.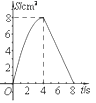
C.
D.
【答案】D
【解析】当0≤t≤4时，S=S正方形ABCD﹣S△ADF﹣S△ABE﹣S△CEF
=4×4﹣ 
×4×（4﹣t）﹣ ×4×（4﹣t）﹣ ×t×t
=﹣ t2+4t
=﹣ （t﹣4）2+8；
当4＜t≤8时，S= （8﹣t）2= （t﹣8）2．
所以答案是：D．
【考点精析】掌握正方形的性质是解答本题的根本，需要知道正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
英才计划期末调研系列答案
相关题目
