题目内容
【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于点A(﹣2,0),交y轴于点B(0,
x2+bx+c与x轴交于点A(﹣2,0),交y轴于点B(0, ![]() ).直线y=kx
).直线y=kx ![]() 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.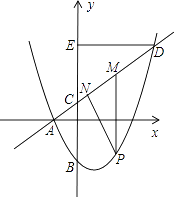
(1)求抛物线y= ![]() x2+bx+c与直线y=kx
x2+bx+c与直线y=kx ![]() 的解析式;
的解析式;
(2)设点P是直线AD下方的抛物线上一动点(不与点A、D重合),过点P作y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为m,点P的横坐标为x,求m与x的函数关系式,并求出m的最大值.
【答案】
(1)
解:∵y= ![]() x2+bx+c经过点A(﹣2,0)和B(0,
x2+bx+c经过点A(﹣2,0)和B(0, ![]() )
)
∴由此得  ,解得
,解得 
∴抛物线的解析式是y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ;
;
∵直线y=kx ![]() 经过点A(﹣2,0)
经过点A(﹣2,0)
∴﹣2k+ ![]() =0,
=0,
解得:k= ![]() ,
,
∴直线的解析式是 y= ![]() x+
x+ ![]()
(2)
解:可求D的坐标是(8,7 ![]() ),点C的坐标是(0,
),点C的坐标是(0, ![]() ),
),
∴CE=6,
设P的坐标是(x, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ),则M的坐标是(x,
),则M的坐标是(x, ![]() x+
x+ ![]() )
)
因为点P在直线AD的下方,
此时PM=( ![]() x+
x+ ![]() )﹣(
)﹣( ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() )=﹣
)=﹣ ![]() x2+
x2+ ![]() x+4,
x+4,
由于PM∥y轴,要使四边形PMEC是平行四边形,必有PM=CE,
即﹣ ![]() x2+
x2+ ![]() x+4=6
x+4=6
解这个方程得:x1=2,x2=4,
当x=2时,y=﹣3,
当x=4时,y=﹣ ![]() ,
,
因此,直线AD下方的抛物线上存在这样的点P,使四边形PMEC是平行四边形,
点P的坐标是(2,﹣3)和(4,﹣ ![]() )
)
(3)
解:在Rt△CDE中,DE=8,CE=6 由勾股定理得:DC= ![]() =10
=10
∴△CDE的周长是24,
∵PM∥y轴,∴∠PMN=∠DCE,
∵∠PNM=∠DEC=90°,∴△PMN∽△CDE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
化简整理得:m与x的函数关系式是:m=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() ,
,
m=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x﹣3)2+15,
(x﹣3)2+15,
∵﹣ ![]() <0,
<0,
∴m有最大值,当x=3时,m的最大值是15.

【解析】(1)把点A、B的坐标分别代入抛物线解析式,列出关于b、c的方程组,通过解方程组可以求得b、c的值;把点A的坐标代入一次函数解析式,列出关于k的方程,通过解方程求得k的值;(2)根据平行四边形的性质推知EC=PM.易求点D的坐标是(8,7 ![]() ),点C的坐标是(0,
),点C的坐标是(0, ![]() ),则CE=6.设P的坐标是(x,
),则CE=6.设P的坐标是(x, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ),则M的坐标是(x,
),则M的坐标是(x, ![]() x+
x+ ![]() ),
),
则PM=( ![]() x+
x+ ![]() )﹣(
)﹣( ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() )=﹣
)=﹣ ![]() x2+
x2+ ![]() x+4,所以由EC=PM得到﹣
x+4,所以由EC=PM得到﹣ ![]() x2+
x2+ ![]() x+4=6,通过解方程求得点P的坐标是(2,﹣3)和(4,﹣
x+4=6,通过解方程求得点P的坐标是(2,﹣3)和(4,﹣ ![]() );(3)通过相似三角形△PMN∽△CDE的性质推知:
);(3)通过相似三角形△PMN∽△CDE的性质推知: ![]() =
= ![]() ,把相关数据代入并整理可以得出m与x的函数关系式是:m=﹣
,把相关数据代入并整理可以得出m与x的函数关系式是:m=﹣ ![]() x2+
x2+ ![]() x+
x+ ![]() =﹣
=﹣ ![]() (x﹣3)2+15,
(x﹣3)2+15,
由抛物线的性质可以得到:m有最大值,当x=3时,m的最大值是15.
【考点精析】解答此题的关键在于理解二次函数的图象的相关知识,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点,以及对二次函数的性质的理解,了解增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
则下列判断正确的是( )
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=4时,y>0
D.方程ax2+bx+c=0的正根在3与4之间




