题目内容
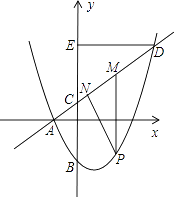
【题目】图中是抛物线拱桥,P处有一照明灯,水面OA宽4m,从O、A两处观测P处,仰角分别为α、β,且tanα= ![]() ,tan
,tan ![]() ,以O为原点,OA所在直线为x轴建立直角坐标系.
,以O为原点,OA所在直线为x轴建立直角坐标系. 
(1)求点P的坐标;
(2)水面上升1m,水面宽多少( ![]() 取1.41,结果精确到0.1m)?
取1.41,结果精确到0.1m)?
【答案】
(1)解:过点P作PH⊥OA于H,如图.
设PH=3x,
在Rt△OHP中,
∵tanα= ![]() =
= ![]() ,
,
∴OH=6x.
在Rt△AHP中,
∵tanβ= ![]() =
= ![]() ,
,
∴AH=2x,
∴OA=OH+AH=8x=4,
∴x= ![]() ,
,
∴OH=3,PH= ![]() ,
,
∴点P的坐标为(3, ![]() )
)
(2)解:若水面上升1m后到达BC位置,如图,
过点O(0,0),A(4,0)的抛物线的解析式可设为y=ax(x﹣4),
∵P(3, ![]() )在抛物线y=ax(x﹣4)上,
)在抛物线y=ax(x﹣4)上,
∴3a(3﹣4)= ![]() ,
,
解得a=﹣ ![]() ,
,
∴抛物线的解析式为y=﹣ ![]() x(x﹣4).
x(x﹣4).
当y=1时,﹣ ![]() x(x﹣4)=1,
x(x﹣4)=1,
解得x1=2+ ![]() ,x2=2﹣
,x2=2﹣ ![]() ,
,
∴BC=(2+ ![]() )﹣(2﹣
)﹣(2﹣ ![]() )=2
)=2 ![]() =2×1.41=2.82≈2.8.
=2×1.41=2.82≈2.8.
答:水面上升1m,水面宽约为2.8米.

【解析】(1)过点P作PH⊥OA于H,如图,设PH=3x,运用三角函数可得OH=6x,AH=2x,根据条件OA=4可求出x,即可得到点P的坐标;(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目