题目内容
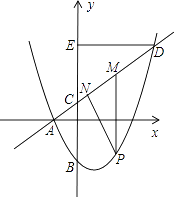
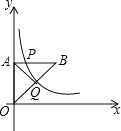
【题目】如图,等腰直角三角形OAB的一条直角边在y轴上,点P是边AB上的一个动点,过点P的反比例函数y= ![]() 的图象交斜边OB于点Q,
的图象交斜边OB于点Q,
(1)当Q为OB中点时,AP:PB=
(2)若P为AB的三等分点,当△AOQ的面积为 ![]() 时,k的值为
时,k的值为 
【答案】
(1)![]()
(2)2或2 ![]()
【解析】解:(1)设Q(m, ![]() ), ∵Q为OB中点,
), ∵Q为OB中点,
∴B(2m, ![]() ),A(0,
),A(0, ![]() ),
),
∴P( ![]() ,
, ![]() ),
),
∴AP:PB= ![]() :(2m﹣
:(2m﹣ ![]() )=
)= ![]() .
.
所以答案是: ![]() .(2)设P(n,
.(2)设P(n, ![]() )(n>0).
)(n>0).
P为AB的三等分点分两种情况:
①AP:PB= ![]() ,
,
∴B(3n, ![]() ),A(0,
),A(0, ![]() ),
),
∴直线OB的解析式为y= ![]() x=
x= ![]() x,
x,
联立直线OB与反比例函数解析式,得: 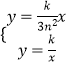 ,
,
解得: 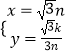 ,或
,或 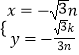 (舍去).
(舍去).
∵S△AOQ= ![]() AOxQ=
AOxQ= ![]() ×
× ![]() ×
× ![]() n=
n= ![]() ,
,
解得:k=2;
②AP:PB=2,
∴B( ![]() n,
n, ![]() ),A(0,
),A(0, ![]() ),
),
∴直线OB的解析式为y= ![]() x=
x= ![]() x,
x,
联立直线OB与反比例函数解析式,得: 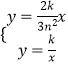 ,
,
解得: 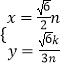 ,或
,或 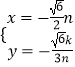 (舍去).
(舍去).
∵S△AOQ= ![]() AOxQ=
AOxQ= ![]() ×
× ![]() ×
× ![]() n=
n= ![]() ,
,
解得:k=2 ![]() .
.
综上可知:k的值为2或2 ![]() .
.
所以答案是:2或2 ![]() .
.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对比例系数k的几何意义的理解,了解几何意义:表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积.

练习册系列答案
相关题目