题目内容
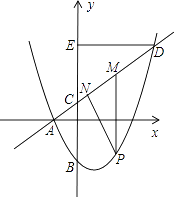
【题目】已知:如图,一次函数y=﹣2x+1与反比例函数y= ![]() 的图象有两个交点A(﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE.
的图象有两个交点A(﹣1,m)和B,过点A作AE⊥x轴,垂足为点E;过点B作BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),连接DE. 
(1)求k的值;
(2)求四边形AEDB的面积.
【答案】
(1)解:如图所示,延长AE,BD交于点C,则∠ACB=90°,
∵一次函数y=﹣2x+1的图象经过点A(﹣1,m),
∴m=2+1=3,
∴A(﹣1,3),
∵反比例函数y= ![]() 的图象经过A(﹣1,3),
的图象经过A(﹣1,3),
∴k=﹣1×3=﹣3;
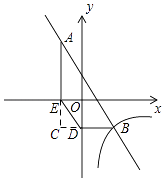
(2)解:∵BD⊥y轴,垂足为点D,且点D的坐标为(0,﹣2),
∴令y=﹣2,则﹣2=﹣2x+1,
∴x= ![]() ,即B(
,即B( ![]() ,﹣2),
,﹣2),
∴C(﹣1,﹣2),
∴AC=3﹣(﹣2)=5,BC= ![]() ﹣(﹣1)=
﹣(﹣1)= ![]() ,
,
∴四边形AEDB的面积=△ABC的面积﹣△CDE的面积
= ![]() AC×BC﹣
AC×BC﹣ ![]() CE×CD
CE×CD
= ![]() ×5×
×5× ![]() ﹣
﹣ ![]() ×2×1
×2×1
= ![]() .
.
【解析】(1)根据一次函数y=﹣2x+1的图象经过点A(﹣1,m),即可得到点A的坐标,再根据反比例函数y= ![]() 的图象经过A(﹣1,3),即可得到k的值;(2)先求得AC=3﹣(﹣2)=5,BC=
的图象经过A(﹣1,3),即可得到k的值;(2)先求得AC=3﹣(﹣2)=5,BC= ![]() ﹣(﹣1)=
﹣(﹣1)= ![]() ,再根据四边形AEDB的面积=△ABC的面积﹣△CDE的面积进行计算即可.
,再根据四边形AEDB的面积=△ABC的面积﹣△CDE的面积进行计算即可.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目