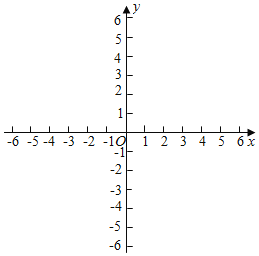Question

【题目】在平面直角坐标系xOy中，已知抛物线y＝ax2+bx﹣1交y轴于点P．

（1）过点P作与x轴平行的直线，交抛物线于点Q，PQ＝4，求的值；

（2）横纵坐标都是整数的点叫做整点．在（1）的条件下，记抛物线与x轴所围成的封闭区域（不含边界）为W．若区域W内恰有4个整点，结合函数图象，求a的取值范围．

Answer 1

【答案】（1）-4或4；（2）＜a≤或﹣1≤a＜﹣．

【解析】

（1）根据题意先求出点Q坐标，代入解析式进行计算即可求解；

（2）根据题意分两种情况讨论，利用特殊点进行分析计算即可求解．

解：（1）∵抛物线y＝ax2+bx﹣1交y轴于点P，

∴点P（0，﹣1），

∵PQ＝4，PQ∥x轴，

∴点Q（4，﹣1），（﹣4，﹣1）

当点Q为（4，﹣1），

∴﹣1＝16a+4b﹣1，

∴，

当点Q（﹣4，﹣1）

∴﹣1＝16a﹣4b﹣1，

∴＝4；

（2）当a＞0时，

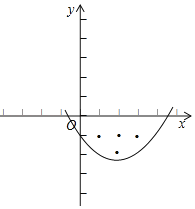
当抛物线过点（2，﹣2）时，a＝，

当抛物线过点（1，﹣2）时，a＝，

∴＜a≤；

当a＜0时，

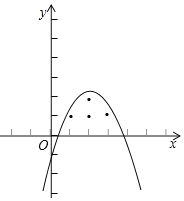
当抛物线过点（2，2）时，a＝﹣，

当抛物线过点（2，3）时，a＝﹣1，

∴﹣1≤a＜﹣，

综上所述：＜a≤或﹣1≤a＜﹣．