题目内容
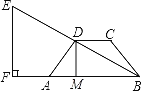
【题目】△ABC中,AB=BC,∠ABC=90°,将线段AB绕点A逆时针旋转α(0°<α<90°)得到线段AD.作射线BD,点C关于射线BD的对称点为点E.连接AE,CE.
(1)依题意补全图形;
(2)若α=20°,直接写出∠AEC的度数;
(3)写出一个α的值,使AE=![]() 时,线段CE的长为
时,线段CE的长为![]() ﹣1,并证明.
﹣1,并证明.
【答案】(1)见解析;(2)∠AEC=135°;(3)α=30°,证明见解析
【解析】
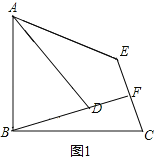
(1)作CF⊥BD并延长CF到E使EF=CF,如图1,
(2)连结BE,如图2,利用对称的性质得BE=BC,则BC=BE=BA,则根据等腰三角形的性质得出∠BCE=∠BEC,∠BAE=∠BEA,由四边形的内角和可计算出∠BCE+∠BEC+∠BAE+∠BEA+∠ABC=360°,进而得到2(∠BEC+∠BEA)=270°,即可证得∠BEC+∠BEA=135°,即∠AEC=135°;
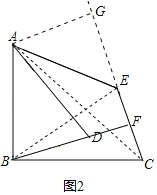
(3)如图2,先证明△AGE为等腰直角三角形,则AG=GE=1,当α=30°时,则∠EBC=30°,进而求得∠ACG=30°,解直角三角形求得CG=![]() ,即可证得CE=CG﹣EG=
,即可证得CE=CG﹣EG=![]() ﹣1.
﹣1.
解:(1)如图1,
(2)∠AEC=135°,
证明:过A作AG⊥CE于G.连接AC、BE,如图2,
由题意,BC=BE=BA,
∴∠BCE=∠BEC,∠BAE=∠BEA,
∵∠BCE+∠BEC+∠BAE+∠BEA+∠ABC=360°
∵∠ABC=90°,
∴2(∠BEC+∠BEA)=270°,
∴∠BEC+∠BEA=135°,即∠AEC=135°,
(3)α=30°,
证明:∵∠AEC=135°,
∴∠AEG=45°,
∵AE=![]() ,
,
∴AG=GE=1,
当α=30°时,
∴∠EBC=30°,
∵BC=BE,
∴∠BCG=75°,
∵∠BCA=45°,
∴∠ACG=30°,
∴![]() ,
,
∴![]() .
.