题目内容
【题目】如果一个圆上所有的点都在一个角的内部或边上,那么称这个圆为该角的角内圆.特别地,当这个圆与角的至少一边相切时,称这个圆为该角的角内相切圆.在平面直角坐标系xOy中,点E,F分别在x轴的正半轴和y轴的正半轴上.
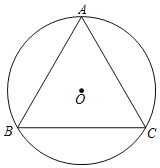
(1)分别以点A(1,0),B(1,1),C(3,2)为圆心,1为半径作圆,得到⊙A,⊙B和⊙C,其中是∠EOF的角内圆的是 ;
(2)如果以点D(t,2)为圆心,以1为半径的⊙D为∠EOF的角内圆,且与直线y=x有公共点,求t的取值范围;
(3)点M在第一象限内,如果存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
)的圆为∠EMO的角内相切圆,直接写出∠EOM的取值范围.
【答案】(1)⊙B,⊙C;(2)1≤t≤2+![]() ;(3)60°≤∠EOM<90°
;(3)60°≤∠EOM<90°
【解析】
(1)画出图象,根据角内相切圆的定义判断即可.
(2)求出两种特殊位置时t的值即可判断.
(3)如图3中,连接OP,OM.首先求出∠POE,根据图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆.
)的圆为∠EMO的角内相切圆.
(1)如图1中,观察图象可知,⊙B和⊙C,其中是∠EOF的角内圆.
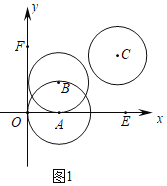
故答案为:⊙B,⊙C.
(2)解:如图,
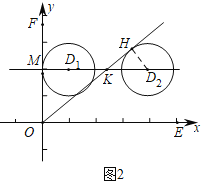
当⊙D1与y轴相切时,设切点为M,则MD1=1,可得t1=1.
当⊙D2与y=x相切时,设切点为H,连接HD2,设直线y=x与直线y=2交于点K,则△HKD2,△MOK都是等腰直角三角形,
∵KH=HD2=1,
∴KD2=![]() ,
,
∵OM=MK=2,
∴MD2=MK+KD2=2+![]()
可得t2=2+![]() ,
,
观察图象可知,满足条件的t的取值范围是1≤t≤2+![]() .
.
(3)如图3中,连接OP,OM.
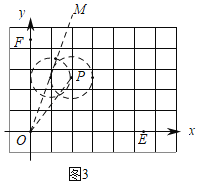
∵P(2,2![]() ),
),
∴tan∠POE=![]() =
=![]() ,
,
∴∠POE=60°,
观察图象可知当射线OM在∠POF的内部(包括射线OP,不包括射线OF)时,存在一个半径为1且过点P(2,2![]() )的圆为∠EMO的角内相切圆,
)的圆为∠EMO的角内相切圆,
∴60°≤∠EOM<90°.

【题目】2020年,由于“疫情”的原因,学校未能准时开学,某中学为了了解学生在家“课间”活动情况,在七、八、九年级的学生中,分别抽取了相同数量的学生对“你最喜欢的运动项目”在线进行调查(每人只能选一项),调查结果的部分数据如下表(图)所示,其中七年级最喜欢跳绳的人数比八年级多5人,九年级最喜欢排球的人数为10人.
七年级学生最喜欢的运动项目人数统计表
项目 | 排球 | 篮球 | 踢毽 | 跳绳 | 其他 |
人数(人) | 7 | 8 | 14 | 6 |
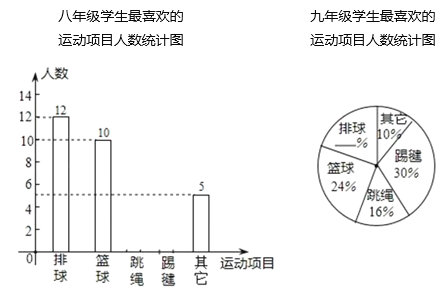
请根据以上统计表(图)解答下列问题:
(1)本次调查共抽取的人数为 人;
(2)请直接补全统计表和统计图;
(3)根据抽样调查的结果,请你估计该校1500名学生中有多少名学生最喜欢踢毽子?